НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1. Формула Тейлора для функции двух переменных.
2. Формула Маклорена.
Напоминание. Формула Тейлора для функции одной переменной 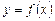 с остаточным членом в форме Лагранжа записывается через дифференциалы этой функции в виде:
с остаточным членом в форме Лагранжа записывается через дифференциалы этой функции в виде:
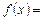
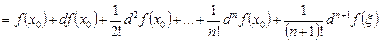 .
.
Теорема 1 (Тейлора). Пусть функция двух переменных 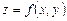 непрерывна со всеми частными производными до
непрерывна со всеми частными производными до 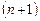 порядка включительно в некоторой
порядка включительно в некоторой 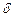 -окрестности точки
-окрестности точки 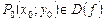 . Тогда справедлива формула формулой Тейлора для функции двух переменных
. Тогда справедлива формула формулой Тейлора для функции двух переменных
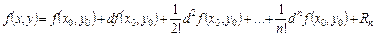 , (1)
, (1)
где 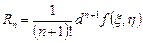 ,
, 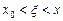 ;
; 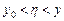 .
.
► Рассмотрим вспомогательную функцию
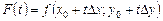 ,
, 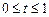 ,
,
которая является сложной функцией независимой переменной 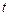 и имеет
и имеет 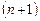 -ю производную по
-ю производную по 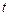 на отрезке
на отрезке 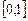 .
.
Согласно формуле Тейлора для функции одной переменной с остаточным членом в форме Лагранжа имеем
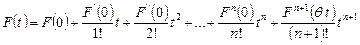 ,
,
(2)
где 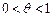 .
.
Отсюда при 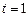 получим
получим
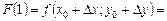
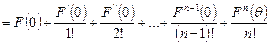 ,
,
где 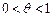 .
.
Найдем производные функции 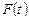 . Так как
. Так как 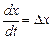 и
и 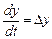 , то первая производная есть:
, то первая производная есть:
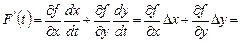
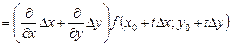 ,
,
вторая –
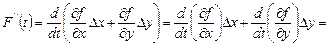
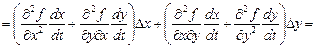
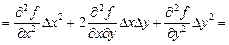
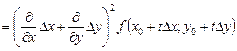 .
.
По индукции получаем:
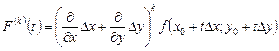 ,
, 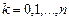 ,
,
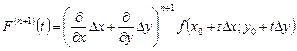 .
.
Тогда
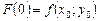 ,
,
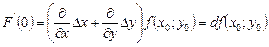 ,
,
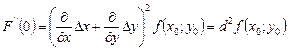 ,
,
…………………………………………………
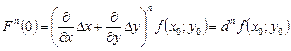 ,
,
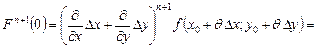
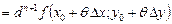 .
.
Подставляя в формулу (2), имеем
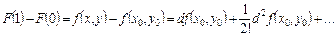
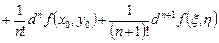 ,
,
где 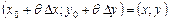 .◄
.◄
Следствие. При условиях теоремы 1 имеет место формула Тейлора с остаточным членом в форме Пеано
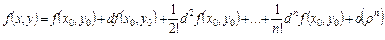 . (3)
. (3)
► Остаточный член формулы Тейлора в форме Лагранжа для функции 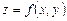
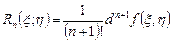
является при 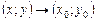 бесконечно малой величиной более высокого порядка малости по сравнению с
бесконечно малой величиной более высокого порядка малости по сравнению с 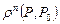 , где
, где 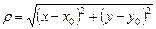 . Поэтому остаточный член
. Поэтому остаточный член 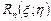 можно представить в форме Пеано
можно представить в форме Пеано
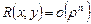 . ◄
. ◄
 2014-02-09
2014-02-09 2161
2161