Формула Маклорена

Если в формуле (1) положить 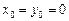, получается формула Маклорена для функции двух переменных :

.

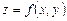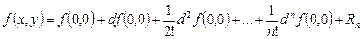Пример. Записать формулу Тейлора при 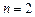с остаточным членом в форме Пеано для функции 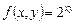в точке .

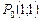Решение. Для любых 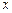, 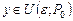имеет место формула Тейлора второго порядка:

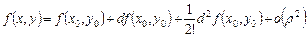
или в краткой записи

.

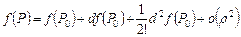Вычислим:

,

,

.

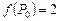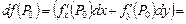
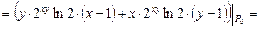
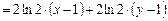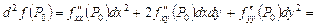
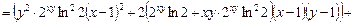
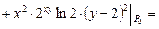
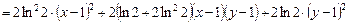Следовательно,

,

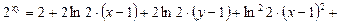
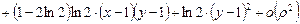где .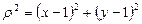

С помощью формулы Тейлора для функции двух независимых переменных можно находить приближенные значения функции в точке, а также исследовать функции двух переменных на экстремум.

Вопросы для самоконтроля

1. Сформулируйте теорему Тейлора для функции двух переменных.

2. Какой вид имеет формула Маклорена для функции двух переменных?