Случайные величины. Дни отмерены нам статистиками

С. Е. Лец

Р. фон Мизес

Дни отмерены нам статистиками…

Математическая статистика – это раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных. Такие данные приносит учет всякого рода массовых явлений и процессов.

Случайная величина – переменная величина, конкретное значение которой зависит от случая. Например, температура воздуха в 12 ч дня 1 июля в г. Новосибирске; номер грани, выпадающий при бросании игрального кубика; скорость автомобиля в данный момент времени и т.д.

Для характеристики случайной величины необходимо знать множество возможных значений этой величины и вероятности, с которыми она может принимать эти значения. Эти данные образуют закон распределения случайной величины. Например, распределение числа очков при бросании игральной кости описывается равными вероятностями 1/6 для каждого значения от 1 до 6.

Различают случайные величины дискретные и непрерывные. Если множество возможных значений случайной величины конечно (или счетно), то случайная величина называется дискретной. Если случайная величина принимает значения из некоторого числового интервала множества действительных чисел, то такая случайная величина называется непрерывной.

Дискретной случайной называют величину X, которая принимает отдельные значения х_i с вероятностями p_i.

В зависимости от типа случайной величины – дискретной или непрерывной – возможны различные способы ее задания. Характеристика повторяемости случайных событий есть его вероятность. Поэтому для наиболее полного, исчерпывающего описания случайной величины надо задавать два множества: множество ее значений и множество вероятностей этих значений. В результате приходим к следующему определению.

Законом распределения дискретной случайной величины Х называется всякое соотношение, устанавливающее связь в виде равенства между возможными значениями случайной величины и вероятностями этих значений.

Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону распределения.

Закон распределения может быть задан в виде ряда, таблицы, аналитически (в виде формулы) и графически.

Непрерывную случайную величину А следует задавать не указанием вероятностей ее отдельных значений, а непрерывной (или кусочно-непрерывной) функцией, называемой плотностью распреде ления вероятностей случайной величины А.

Часто встречается нормальное распределение, или распределение Гаусса. На рисунке показаны два варианта плотности нормального распределения.

Важные характеристики случайной величины – математическое ожидание и дисперсия.

Математическое ожидание М(Х) определяется как среднее взвешенное по формуле .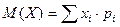

Термин «математическое ожидание» связан с представлением о среднем или наиболее ожидаемом выигрыше в теории азартных игр.

Пример 1. Пусть в некоторой лотерее на каждый билет вероятность выиграть 100 руб. – 3%, 1 000 руб. – 0,5%, 10 000 руб. – 0,01%, других выигрышей нет. Каков средний выигрыш в лотерее (на один билет)?

Решение.Средний выигрыш подсчитывается по формуле математического ожидания

0,03x100 + 0,005x1000 + 0,0001x10 000 = 9 руб.

Дисперсия ( от лат. dispengo – рассыпать, рассеивать, разбрасывать ) D(X) случайной величины X характеризует разброс возможных ее значений относительно математического ожидания и определяется по формуле D(X) = М[Х – М (X)]².

Для детерминированной величины, принимающей только одно значение х₀, математическое ожидание равно х₀, а дисперсия равна нулю.

Понятие случайного (стохастического) процесса является расширением понятия случайной величины. Можно сказать, что случайный процесс – это семейство случайных величин, эволюционирующих во времени.