Сила Лоренца

Магнитное поле в вакууме. Магнитная индукция.

1. По современным представлениям движущиеся заряды и электрические токи создают в окружающем пространстве магнитное поле, которое как особый вид материи, хотя и не действует на органы чувств человека, но проявляет себя в силовом воздействии на другие токи и движущиеся заряды. Магнитное поле постоянных магнитов связано с движением электронов в атомах и молекулах.

В этой теме мы будем сначала рассматривать постоянное магнитное поле в вакууме, создаваемое стационарным движением зарядов и постоянными токами, а затем перейдем к исследованию поля в веществе.

Для описания магнитного поля необходимо ввести количественные характеристики. Одной из таких характеристик является индукция магнитного поля - 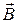. Это – силовая характеристика магнитного поля.

Опыты показывают, что магнитные стрелки в одной и той же точке поля всегда устанавливаются в одном и том же направлении. Направление северного конца магнитной стрелки в данной точке принимается за направление этой силовой характеристики.

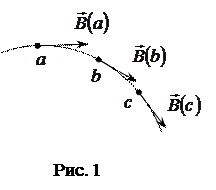
Для магнитного поля, также как для электрического, вводятся силовые линии, касательная к которым совпадает с направлением вектора 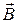в любой точке. Пример силовой линии приведен на рис. 1, на котором показано это ее основное свойство. Через любую точку поля проходит только одна силовая линия, так как в любой точке существует только одно направление вектора 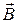. В однородном магнитном поле силовые линии представляют собой параллельные прямые.

2. Для введения величины вектора магнитной индукции необходима еще одна операция: опытное исследование силового действия магнитного поля. В качестве датчиков, регистрирующих такое воздействие, можно выбирать магнитные стрелки, отрезки проводников с токами или движущиеся заряды. Требования к датчику магнитного поля, в общем такие же, как к датчикам электрического поля. Датчик должен быть мал по размерам, чтобы можно было с его помощью фиксировать магнитное поле в точке. Датчик должен легко калиброваться, с тем, чтобы характеристики самого датчика были постоянными во времени и легко контролируемыми.

С точки зрения этих требований магнитные стрелки не обладают постоянными свойствами, их характеристики трудно контролировать. Рамки с токами не могут быть сделаны достаточно малыми по размерам. Бесконечно малый элемент тока нельзя выделить из проводника и поэтому освободиться от механического воздействия на него окружающих частей провода. С этой точки зрения наиболее приемлемым датчиками магнитного поля являются движущиеся заряды. Величину заряда и его скорость можно делать достаточно воспроизводимыми. Но и этот датчик обладает недостатком. Заряд движется, и, значит, силовое воздействие на него в данной точке пространства должно быть зафиксировано за малый промежуток времени. Несмотря на этот недостаток, мы останавливаемся на этом датчике, так как его использование позволяет более логично излагать учебный материал.

3. Прежде чем приступить к изучению силового действия магнитного поля с помощью движущихся электрических зарядов необходимо убедиться в отсутствии электрических полей, которые сами действуют на заряженную частицу силой, пропорциональной напряженности электрического поля

.

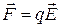Если через одну и ту же точку магнитного поля с известным направлением вектора 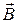пропускать разные заряженные частицы и определять силы, действующие на них, то эти опыты показывают следующие результаты. Направление силы, действующей на частицу, перпендикулярно векторам 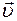и 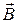и определяется по правилу правого буравчика. 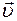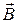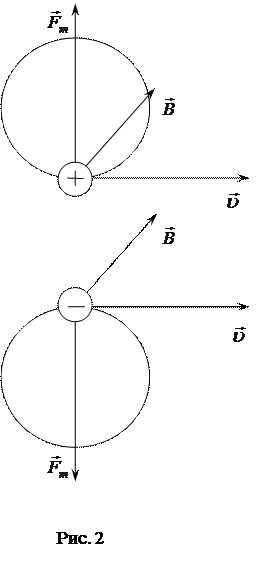Если поворачивать рукоятку буравчика от направления вектора к направлению вектора на наименьший угол, то поступательное движение буравчика будет совпадать с направлением вектора силы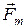, действующей на положительно заряженную частицу. Для отрицательно заряженной частицы направление силы будет противоположным (рис. 2). Величина силы пропорциональна величинам заряда, скорости частицы и синусу угла a между направлениями векторов 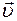и

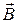
F_m ~ .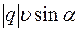

Теперь мы можем определить величину магнитной индукции следующим образом. Пусть угол a = 90⁰(частица движется перпендикулярно силовой линии). Опыт показывает, что отношение силы, действующей на частицу в данной точке, к величине произведения 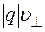не зависит от ее заряда и скорости и принимается за величину вектора 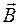в данной точке пространства

.

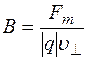Единица магнитной индукции 1 тл вводится через магнитный поток.

4. Магнитное поле определено, если для каждой точки пространства известна величина и направление магнитной индукции. По известной индукции магнитного поля можно рассчитывать силу, действующую на движущуюся заряженную частицу

.

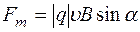С учетом пространственной ориентации векторов 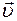, 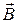и 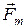можем записать для силы, действующей со стороны магнитного поля, выражение

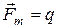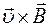[]. (1)

Полная сила, действующая на заряженную частицу со стороны электрического и магнитного полей, называется силой Лоренца и записывается в виде

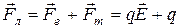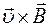[]. (2)

Сила Лоренца по своей природе является единой силой, а разделение ее на две силы, из которых одна 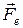действует со стороны электрического поля, а другая 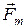- со стороны магнитного поля, носит условный характер.

Так как 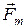зависит от скорости движения частицы, а сама скорость от выбора системы отсчета, то 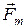имеет относительный характер, т.е. зависит от выбранной системы отсчета. Поэтому, чтобы сила Лоренца оставалась одинаковой в разных системах отсчета (при малых скоростях движения), должна иметь относительный характер и сила 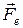. В системе отсчета 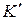, движущейся со скоростью 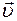, относительно которой частица покоится (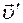= 0), магнитная составляющая силы Лоренца также будет равна нулю (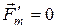), а в неподвижной системе отсчета K она определяется выражением (2). Поэтому

[].

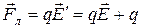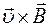Отсюда находим, что напряженность электрического поля 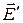в системе отсчета 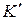будет равна

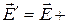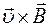[]. (3)

Это означает, что напряженность электрического поля имеет относительный характер и зависит от выбора системы отсчета. Электрическое и магнитное поля не являются независимыми, а переходят друг в друга при изменении системы отсчета.

5. В теории относительности доказано, что характеристики магнитного поля в вакууме также имеют относительный характер и изменяются при переходе от неподвижной системы отсчета к подвижной. Например, для векторов магнитной индукции имеет место соотношение (при условии )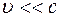

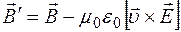. (4)

Формулы (3), (4) устанавливают законы преобразования характеристик полей от неподвижной системы отсчета K к подвижной 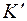. С равным правом можно считать систему 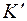неподвижной, а систему K движущейся в отрицательном направлении оси 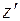со скоростью 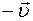и записать соотношения

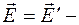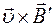[], (5)

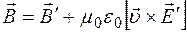, (6)

которые справедливы также как и формулы (3), (4) для медленных движений (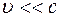), с точностью до членов, содержащих 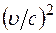. Здесь 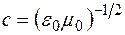- скорость света в вакууме.

Величины 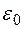и 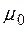, входящие в формулы (4, 6) являются электрической и магнитной постоянными СИ. Их величины и размерность обусловлены выбором единиц измерения.

Выводы.

1. Направление вектора 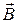в данной точке совпадает с направлением северного полюса свободной магнитной стрелки, помещенной в эту точку.

2. Вектор магнитной индукции численно равен отношению силы к произведению величин заряда и составляющей скорости, перпендикулярной силовым линиям .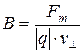

3. На движущуюся в магнитном поле заряженную частицу действует сила, определяемая формулой [].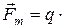

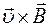4. Разделение силы Лоренца на электрическую и магнитную носит относительный характер и поэтому относительный характер имеет и магнитная индукция.