2014-02-09
1823
Электрическая модель биполярного транзистора в статическом режиме была предложена Эберсом и Моллом на основе суммы уравнений (6.7) и (6.10) для токов через p-n -переходы в нормальном активном и инверсном режимах работы (рис. 6.4).
Из схемы следует, что
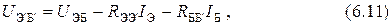
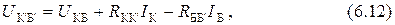
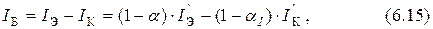
где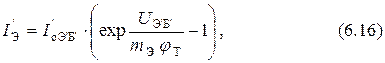 
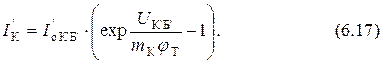
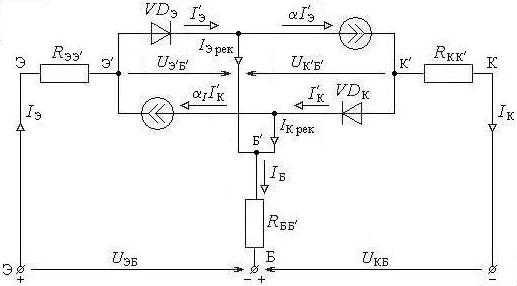
Рис. 6.4. Модель Эберса-Молла для БТ p-n-p -типа
В формулы (6.16) и (6.17) независимо от типа транзистора (p-n-p или n-p-n) напряжения подставляют со знаком плюс при прямом включении диода и со знаком минус – при обратном. Положительным направлением тока диода считают прямое направление тока, то есть направление от p - к n -области.
При нормальном активном режиме ток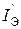 
, созданный открытым эмиттерным переходом, много больше тока 
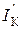, созданного закрытым коллекторным переходом. При инверсном активном режиме ток 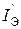мал, так как создаётся закрытым эмиттерным переходом, а ток 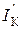велик потому, что создаётся открытым коллекторным переходом.
Подставляя выражения (6.16) и (6.17) в уравнения (6.13) ÷ (6.15), получаем
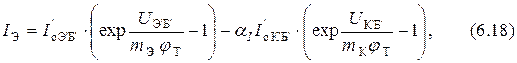
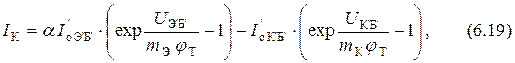
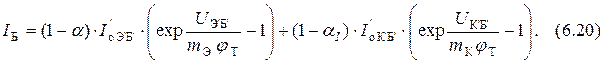
В модели использованы внутренние недоступные точки транзистора. Поэтому необходимо уравнения (6.18) ÷ (6.20) преобразовать так, чтобы выразить внутренние параметры через внешние, доступные для измерения. Это можно сделать, проведя специальные измерения.
|
|
|
Анализ специальных измерений позволяет получить выражения
Кроме того, обычно выполняется условие обратимости:
Решая совместно уравнения (6.18) и (6.19), находим
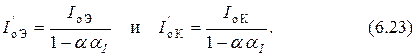
Исключая последовательные сопротивления ветвей, то есть, принимая в выражениях (6.12) и (6.13) соотношения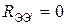 
, 
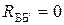и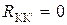 
, получаем равенства 
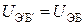и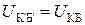 
. С учётом этого и выражений (6.23) находим преобразованные уравнения
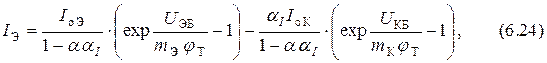
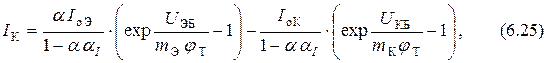
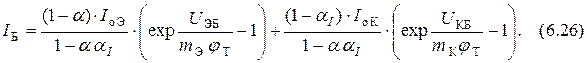
Уравнения (6.24) ÷ (6.26) попарно представляют собой уравнения транзистора в Y-параметрах, записанные в трансцендентной (неявной) форме.
Эти уравнения описывают основную (простейшую) модель Эберса-Молла биполярного транзистора (рис. 6.5).
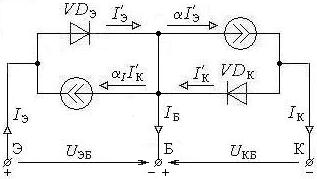
Рис. 6.5. Простейшая модель Эберса-Молла для БТ p-n-p -типа
