Транзитивность

Связность (полнота).

Асимметричность.

Отношение называется асимметричным, если для всех x выполняется условие: xjy Þù yjx или 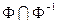=Æ.

Отношение называется связным (полным), если для всех x выполняется условие: x¹y Þ xjy или yjx или М²\DMÍ.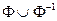

Отношение называется транзитивным, если для всех x выполняется условие: xjy и yjz Þ xjz или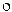 ФФÍФ.

ПРИМЕР

Какими свойствами обладает отношение j=<Ф,X>, где X={1; 2; а},

Ф={<1,1>;<a,a>;<a,2>;<2,2>}.

Определим Ф^-1, DX:

Ф^-1={<1,1>;<a,a>;<2,a>;<2,2>}

DX={<1,1>;<2,2>;<a,a>}.

Отношение является:

- рефлексивным, так как DXÍФ;

- антисимметричным, так как 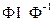ÍDX;

- транзитивным, так как Ф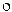Ф={<1,1>;<a,a>;<a,2>;<2,2>}ÍФ;

- несвязное, так как X²\DX={<1,2>;<1,a>;<2,1>;<2,a>;<a,1>;<a,2>}Ë Ф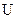Ф^-1={<1,1>;<a,a>;<a,2>;<2,2>;<2,a>}.

Отношение называется отношением эквивалентности, если оно рефлексивное, симметричное и транзитивное.

Отношение называется отношением нестрогого (частичного) порядка (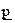),если оно рефлексивное, антисимметричное и транзитивное.

Отношение называется совершенно нестрого порядка (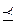),если оно рефлексивное, антисимметричное, транзитивное и связное.

Отношение называется строго порядка (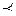),если оно антирефлексивное, антисимметричное и транзитивное.

Отношение называется совершенно строго порядка (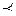),если оно антирефлексивное, транзитивное и связное.