2014-02-09
514
Лекция 9. Матрицы
Контрольные вопросы к теме
- Понятие евклидова пространства.
- Линейная зависимость и линейная независимость векторов.
- Понятия размерности и базиса линейного пространства.
- Линейное преобразование векторов.
Основные понятия, включенные в систему тренинг- тестирования:
матрица; элемент матрицы; размер матрицы; строка; столбец; квадратная матрица; главная диагональ; побочная диагональ; диагональная матрица; скалярная матрица; единичная матрица; нулевая матрица; сумма матриц; произведение матриц; согласованные матрицы; транспонирование матриц; определитель матрицы; минор; алгебраическое дополнение; линейная зависимость; линейная комбинация; ранг матрицы; окаймляющий минор; элементарные преобразования матрицы; обратная матрица.
Прямоугольная таблица
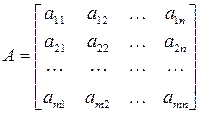
| (9.1) |
состоящая из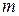 
строк и 
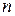столбцов, называется матрицей размера 
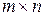или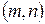 
-матрицей.
Матрицу (9.1) будем обозначать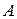 
или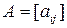 
. Числа 
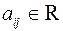называются элементами матрицы, индекс 
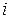обозначает номер строки, а индекс 
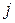‑ номер столбца, на пересечении которых расположен элемент.
Если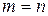 
, то матрица (9.1) называется квадратной матрицей порядка .
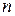В квадратной матрице 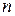-го порядка диагональ, состоящая из элементов 
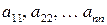называется главной диагональю, состоящая из элементов 
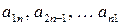‑ побочной диагональю.
Квадратная матрица
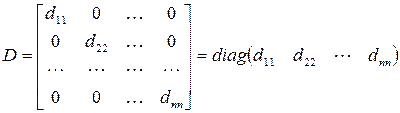
называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е.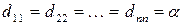 
, то такая матрица называется скалярной. Скалярная матрица, у которой 
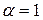называется единичной и обозначается буквой 
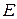. Например, единичная матрица третьего порядка:
.
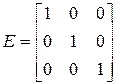Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы 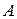и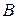 
называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
