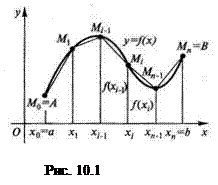
 Пусть дана плоская кривая
Пусть дана плоская кривая 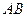 (рис. 10.1), уравнение которой
(рис. 10.1), уравнение которой  ,
, 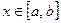 , где
, где 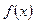 — непрерывно дифференцируемая функция на отрезке
— непрерывно дифференцируемая функция на отрезке 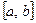 . Разобьем отрезок
. Разобьем отрезок 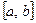 точками
точками 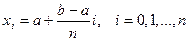 , на
, на 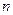 частей равной длины. Через точки деления
частей равной длины. Через точки деления 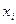 проведем прямые, параллельные оси ординат
проведем прямые, параллельные оси ординат 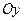 . Точки пересечения этих прямых с кривой
. Точки пересечения этих прямых с кривой 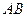 обозначим через
обозначим через 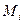 . Соединив эти точки хордами, получим ломаную
. Соединив эти точки хордами, получим ломаную 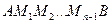 , вписанную в кривую
, вписанную в кривую 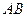 . Пусть периметр этой ломаной равен
. Пусть периметр этой ломаной равен 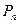 . Длиной дуги
. Длиной дуги 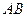 будем называть число
будем называть число  , равное пределу последовательности периметров
, равное пределу последовательности периметров 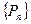 :
:
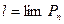
Выведем формулу для вычисления длины дуги. Для этого сначала найдем периметр ломаной 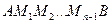 . Точка
. Точка  с координатами
с координатами 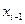 и
и  и точка
и точка 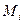 с координатами
с координатами 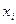 и
и 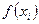 являются концами
являются концами  го звена ломаной. Длину
го звена ломаной. Длину  го звена вычислим по формуле расстояния между двумя точками плоскости:
го звена вычислим по формуле расстояния между двумя точками плоскости:
 . (10.3)
. (10.3)
Учитывая, что 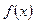 – непрерывная дифференцируемая функция на отрезке
– непрерывная дифференцируемая функция на отрезке 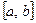 ,по формуле Лагранжа имеем
,по формуле Лагранжа имеем
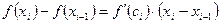 , (10.4)
, (10.4)
где 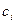 — некоторая точка интервала
— некоторая точка интервала  . Подставив выражение (10.4) в формулу (10.3), получим:
. Подставив выражение (10.4) в формулу (10.3), получим:
 , (10.5)
, (10.5)
где  . Значит, периметр ломаной
. Значит, периметр ломаной 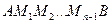 равен следующей сумме:
равен следующей сумме:
 .
.
Получили интегральную сумму для непрерывной функции 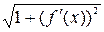 на отрезке
на отрезке 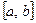 . Так как предел этой суммы при n → ∞ существует, то согласно определению находим
. Так как предел этой суммы при n → ∞ существует, то согласно определению находим
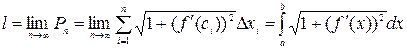 .
.
Таким образом,
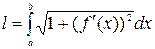
 2014-02-09
2014-02-09 762
762








