Полнота и замкнутость

Примеры.

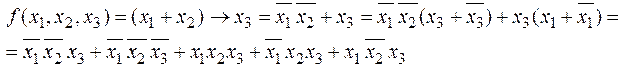
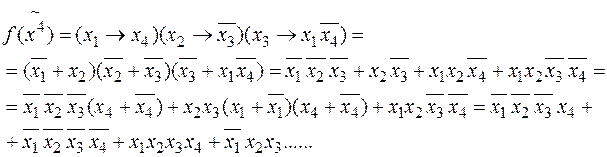
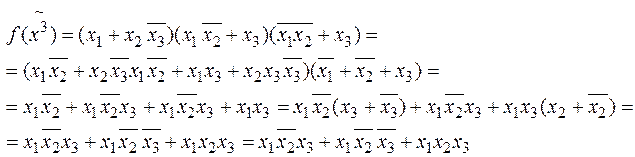
Определение. Система функций В =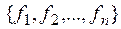из P ₂ (множества всех булевых функций) называется функционально полной, если любая булева функция может быть записана в виде формулы через функции этой системы, т.е. является суперпозицией функций из B.

Примеры.

1) Само множество ;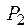

2);

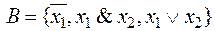Функционально полной будет любая система функций, через функции которой можно выразить &, Ú, .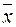

3)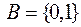– не полна, так как нельзя выразить, например, x.

Теорема. Пусть даны две системы функций из :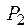

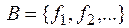, (I)

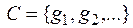. (II)

Известно, что система I полная и каждая функция системы I выражается через функции системы II. Тогда система II является полной.

Доказательство. Пусть 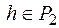. В силу полноты системы I функцию h можно выразить в виде формулы 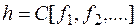. По условию теоремы

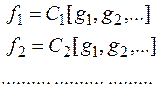
Поэтому

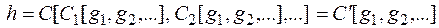что и требовалось доказать.

Примеры.

1) 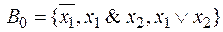– полная. B ₀ – базовая система функций.

2) 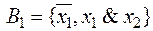– тоже полная, так как недостающая функция.

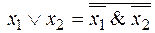3) 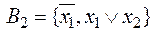– тоже полная, так как .

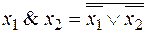4) 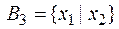и 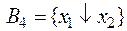– тоже полные, так как

, ,

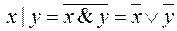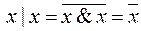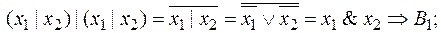
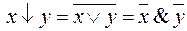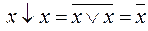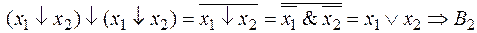5) 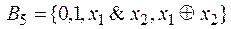функционально полная, так как

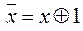, и, следовательно, B ₅ сводится к B ₁.

Алгебра над множеством логических функций с двумя бинарными операциями Å и & называется алгеброй Жегалкина.

В алгебре Жегалкина выполняются следующие соотношения:

x Å y = y Å x,

x & (y Å z) = x & y Å x & z,

x Å x = 0, x Å 0= x,

Отрицание и дизъюнкция выражаются через Å и &:

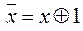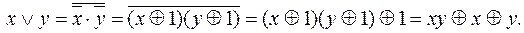
Произвольную формулу алгебры Жегалкина можно представить в виде суммы произведений, т.е. полинома по модулю 2. Такая формула называется полиномом Жегалкина для данной функции.

Теорема Жегалкина. Каждая функция из 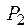может быть выражена при помощи полинома по модулю 2 – (полинома Жегалкина), причем единственного.

Доказательство. Множество P ₂ является функционально полной системой функций. Любая функция из P ₂ может быть представлена формулой над 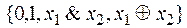, которая после раскрытия скобок и приведения подобных членов дает полином Жегалкина.

Число различных полиномов Жегалкина от n переменных равно числу вариаций вида:

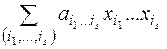Число разных сочетаний 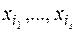равно числу всех подмножеств множества 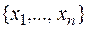из n элементов, т.е. 2 ⁿ. Каждый набор входит с коэффициентом 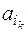, принимающим одно из 2-х значений {0,1}. Тогда число всевозможных полиномов Жегалкина от n переменных будет равно 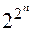, т.е. равно числу различных булевых функций от n переменных.