2014-02-09
901
Полнота и замкнутость
Разложение булевых функций по переменным.
Лекция №9
Место и роль ППФП в системе НОТ.
Говоря о месте и роли ППФП в системе НОТ, мы, по сути дела, рассматриваем проблему использования средств физической культуры и спорта для решения задач, позволяющих наилучшим образом соединить технику и людей в едином производственном процессе.
Проблема ППФП студентов, в связи с научной организацией их будущего труда, состоит в то, что все задачи НОТ могут быть сгруппированы следующим образом:
· экономические задачи, т.е. использование материальных, трудовых и денежных ресурсов;
· психофизиологические задачи, т.е. создание на производстве наиболее благоприятных условий труда и сохранения здоровья и трудоспособности;
· социальные задачи, т.е. обеспечение условий роста культурно-технического уровня работников, всестороннего и гармоничного развития.
Эти задачи реализуются через основные направления НОТ, в которых место и роль ППФП далеко не одинаковы. Наиболее существенное значение профессионально-прикладная подготовка имеет при разработке таких направлений НОТ, какими являются: подготовка и повышение квалификации кадров, рационализация приемов и методов труда.
Следующими направлениями НОТ, с которыми ППФП специалистов имеет тесную и непосредственную связь, являются улучшение условий труда на производстве и рационализация режимов труда и отдыха (продолжительность рабочего времени, напряженность труда, комфортность производственной среды, охрана труда и техника безопасности).
Возникают вопросы:
1) всякая ли функция может быть записана с помощью формулы?
2) как это сделать?
Теорема. Каждая функция алгебры логики может быть выражена в виде так называемой нормальной формы – формулы, содержащей только отрицание, конъюнкцию и дизъюнкцию.
Доказательство.
1) Если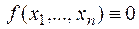 
, то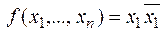 
.
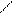2) Если 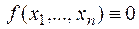, то
.
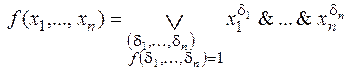Таким представлением функции может служить ее совершенная дизъюнктивная нормальная форма (СДНФ).
Определение. Совершенной дизъюнктивной нормальной формой называется разложение в виде суммы произведений всех n переменных или их отрицаний. (Если не все переменные, то это ДНФ).
Примеры.
1. Дана функция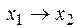
– импликация (табл. 9.1).
Таблица 9.1
Табличный способ представления импликации
| x 1 | x 2 | f |
СДНФ функции f содержит ровно столько конъюнкций, сколько единиц в таблице f. Каждая комбинация произведений дает 1 в единственном случае, когда переменная без отрицания равна 1, а с отрицанием равна 0. Для данного примера СДНФ
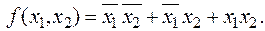
После преобразования имеем
.
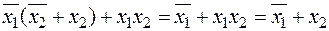2. Задана функция f в табличном виде (табл. 9.2). Представим ее в СДНФ.
Таблица 9.2
Таблица истинности функции f
| x 1 | x 2 | x 3 | f |
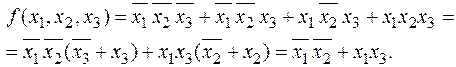
После преобразования СДНФ получаем ДНФ.
3. Исходная функция задана в векторном виде
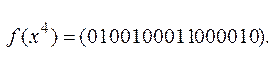
Сопоставим каждому значению функции определенный набор переменных (табл. 9.3) и разложим по переменным, т.е. выразим в виде СДНФ
.
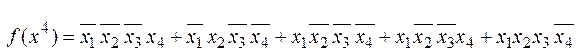Таблица 9.3
Таблица истинности функции f
| x 1 | x 2 | x 3 | x 4 | f |
Определение. Разложение в виде произведений сумм называется совершенной конъюнктивной нормальной формой (СКНФ).
СКНФ функции f содержит ровно столько дизъюнкций, сколько 0 в таблице f. Каждому нулевому набору соответствует дизъюнкция всех переменных, в которой xi взято с отрицанием, если переменная равна 1 и наоборот.
Примеры.
1. (См. табл. 9.1)
.
2. (См. табл. 9.2)
.
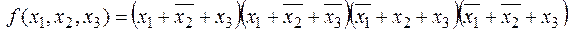3. 
.
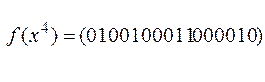Используя табличное представление данной функции (табл. 9.3) получаем следующее разложение (СКНФ):
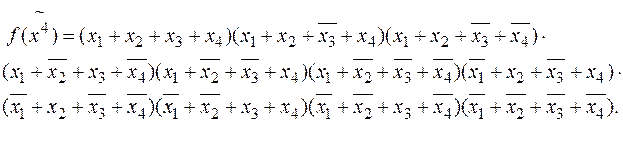
Алгоритм приведения логической функции к дизъюнктивной нормальной форме (ДНФ):
- записать функцию с использованием только операций дизъюнкции, конъюнкции и отрицания;
- с помощью законов де Моргана операцию отрицания довести до отдельных переменных и убрать двойные отрицания;
- с помощью первого закона дистрибутивности убрать все конъюнкции дизъюнкций и провести поглощение.
Для получения КНФ следует изменить третий пункт алгоритма:
- с помощью второго закона дистрибутивности убрать все дизъюнкции конъюнкций и провести поглощение.
В СДНФ все конъюнкции содержат все логические переменные или их отрицания. Аналогично, в СКНФ все дизъюнкции содержат все логические переменные или их отрицания. Поэтому для приведения к совершенным формам необходимы дополнительные преобразования по введению недостающих логических переменных.
