Введение в алгоритм

Пирамидальная сортировка

Анализ времени работы сортировки слиянием через геометрическую интерпретацию

На каждом из уровней рекурсии количество сортируемых элементов не изменяется. Известно также, что при слиянии отсортированных массивов каждый элемент проходит через «соревнование» курсоров, копируясь в целевой массив. Это означает, что суммарные затраты на перемещение элементов разными ветками рекурсии по срезу одной глубины будут равны. Если отбросить связи между элементами в рассматриваемом дереве рекурсии, то оно может быть вписано в прямоугольник с основанием шириной n (размер входа, т.е. количество элементов исходного массива), где n – количество элементов на входе алгоритма. Высота же прямоугольника будет равна высоте дерева, т.е. log n. Таким образом, временные затраты на обратный ход рекурсии составят n · log n. Прямой ход рекурсии не требует столь большого количества вычислительных ресурсов (там нет перемещения элементов из массива в массив), но, тем не менее, количество вызовов прямо пропорционально объему массива, а, следовательно, также описывается как n · log n, пусть и с меньшей константой. Аналогичным способом может оцениваться время работы любой сортировки сравнениями, работающей по принципу «разделяй и властвуй».

n0 n1 n2 n3 n4 n5 n6 n7 n8 n9 n10 n11 n12 n13 n14 n15

n0 n1 n2 n3 n4 n5 n6 n7

n8 n9 n10 n11 n12 n13 n14 n15

n0 n1 n2 n3

n4 n5 n6 n7

n8 n9 n10 n11

n12 n13 n14 n15

n0 n1

n2 n3

n4 n5

n6 n7

n8 n9

n10 n11

n12 n13

n14 n15

n0

n1

n2

n3

n4

n5

n6

n7

n8

n9

n10

n11

n12

n13

n14

n15

Рисунок 2.3 – Геометрическая интерпретация алгоритма сортировки слиянием

Как и алгоритм сортировки слиянием, алгоритм пирамидальной сортировки требует времени О (п· log п)для сортировки п объектов, но обходится дополнительной памятью размера О (1) (вместо О (п)для сортировки слиянием). Таким образом, этот алгоритм сочетает преимущества двух ранее рассмотренных алгоритмов – сортировки слиянием и сортировки вставками.

Структура данных, которую использует алгоритм (она называется двоичной кучей) оказывается полезной и в других ситуациях. В частности, на её базе можно эффективно организовать очередь с приоритетами.

Термин «куча» иногда используют в другом смысле (область памяти, где данные размещаются с применением автоматической «сборки мусора» – напри­мер, в языках Lisp и C#).

Двоичной кучей (binary heap) называют массив с определёнными свойства­ми упорядоченности. Чтобы сформулировать эти свойства, будем рассматривать массив как двоичное дерево (рис. 2.3). Каждая вершина дерева соответствует элементу массива. Если вершина имеет индекс i, то её родитель имеет индекс 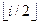(вершина с индексом 1 является корнем), а её дети – индексы (2× i) и (2× i + 1). Т.к. куча может не занимать всего массива, и поэтому нужно хранить не только массив А и его длину length [ A ], но также специальный па­раметр heap-size [ A ](размер кучи), причём heap-size [ A ] ≤ length [ A ]. Куча состоит из элементов А [1] ,..., A [ heap-size [ A ]]. Движение по дереву осуществляется процедурами:

Листинг 2.3 – Процедуры перемещения по дереву (реализация на базе массива)

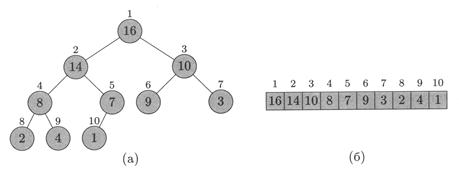
Рисунок 2.3 – Интерпретации кучи: как дерево (а) или как массив (б)

Элемент А [1] является корнем дерева. В большинстве компьютеров для выполнения процедур Left и Parent можно использовать команды левого и правого сдвига (Left, Parent); Right требует левого сдвига, после которого в младший разряд помещается единица. Элементы, хранящиеся в куче, должны обладать основным свойством кучи (heap property): для каждой вершины i, кроме корня (т.е. при 2 ≤ i ≤ heap-size [ A ]),

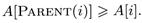
Отсюда следует, что значение потомка не превосходит значения предка. Та­ким образом, наибольший элемент дерева (или любого поддерева) находится в корневой вершине дерева (этого поддерева).

Высотой (height) вершины дерева называется высота поддерева с корнем в этой вершине (число рёбер в самом длинном пути с началом в этой вершине вниз по дереву к листу). Высота дерева, таким образом, совпадает с высотой его корня. В дереве, составляющем кучу, все уровни (кроме, быть может, по­следнего) заполнены полностью. Поэтому высота этого дерева равна Θ(log n), где п – число элементов в куче. Время работы основных операций над кучей пропорционально высоте дерева и, следо­вательно, составляет O (log n). Оставшаяся часть главы посвящена анализу этих операций и применению кучи в задачах сортировки и моделирования очереди с приоритетами. Перечислим основные операции над кучей.

• Процедура Heapify позволяет поддерживать основное свойство («ребенок не больше своего родителя»). Время работы составляет O (log n).

• Процедура Build-Heap строит кучу из исходного (неотсортированного) мас­сива. Время работы O (п).

• Процедура HeapSort сортирует массив, не используя дополнительной памя­ти. Время работы O (n ×log n).

• Процедуры Extract-Max (взятие наибольшего) и Insert (добавление эле­мента) используются при моделировании очереди с приоритетами на базе кучи. Время работы обеих процедур составляет O (log n).