Построение минимального покрывающего дерева

Итак, пусть дан связный неориентированный граф G = (V, Е) и весовая
функция w: Е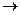R. Мы хотим найти минимальное покрывающее дерево (мини-
мальный остов), следуя жадной стратегии.

Общая схема всех наших алгоритмов будет такова. Искомый остов строится
постепенно: кизначально пустому множеству А на каждом шаге добавляется
одно ребро. Множество А всегда является подмножеством некоторого мини-
мального остова. Ребро (u, v), добавляемое на очередном шаге, выбирается так,
чтобы не нарушить этого свойства: 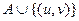тоже должно быть подмноже-
ством минимального остова. Мы называем такое ребро безопасным ребром (safe
edge) для А.

Листинг 5.8 – Общий алгоритм построения минимального покрывающего дерева

По определению безопасного ребра свойство «А является подмножеством
некоторого минимального остова» остаётся истинным после любого числа ите-
раций цикла (для пустого множества это свойство, очевидно, выполнено), так
что в строке 5 алгоритм выдаёт минимальный остов. Конечно, главный вопрос
состоит в том, как искать безопасное ребро в строке 3. Такое ребро существует
(если А является подмножеством минимального остова, то любое ребро этого
остова, не входящее в А, является безопасным).

Заметим, что множество А не может содержать циклов (поскольку является
частью минимального остова). Поэтому добавляемое в строке 4 ребро соеди-
няет различные компоненты графа G _А = (V, A), и с каждой итерацией цикла
число компонент уменьшается на 1. Вначале каждая точка представляет собой
отдельную компоненту; в конце весь остов одна компонента, так что цикл
повторяется | V | – 1 раз.

В оставшейся части этого раздела будет приведено правило отыскания безопас-
ных рёбер. В следующем разделе будут описаны два алгоритма,
использующих это правило для эффективного поиска безопасных рёбер.

Начнём с определений. Разрезом (cut) (S, V \ S) неориентированного графа
G = (V, E) называется разбиение множества его вершин на два подмножества
(рис. 5.7).

Говорят, что ребро (и, v) 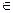Е пересекает (crosses) разрез (S, V \ S), если
один из его концов лежит в S, а другой – в V \ S. Разрез согласован с множе-
ством рёбер А (respects the set А), если ни одно ребро из А не пересекает этот
разрез. В множестве пересекающих разрез рёбер выделяют ребра наименьшего
(в этом множестве) веса, называя их лёгкими (light edges).

Теорема 5.8. Пусть G = (V, Е) – связный неориентированный граф, на множе-
стве вершин которого определена вещественная функция w. Пусть А – мно-
жество рёбер, являющееся подмножеством некоторого минимального остова
графа G. Пусть (S, V \ S) – разрез графа G, согласованный с А, а(u, v) – лёгкое
ребро для этого разреза. Тогда ребро (u, v) является безопасным для А.

Доказательство. Пусть Т – минимальный остов, содержащий А. Предположим,
что Т не содержит ребра (и, v), поскольку в противном случае доказываемое
утверждение очевидно. Покажем, что существует другой минимальный остов Т ',
содержащий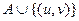, так что ребро (и, v)является безопасным для А.

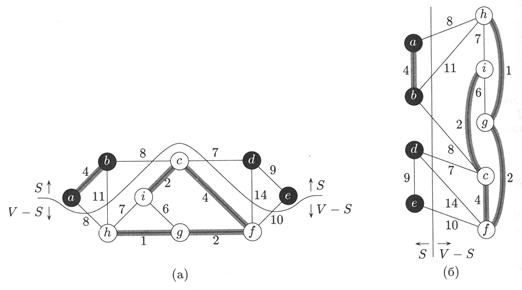
Рисунок 5.7 – Два изображения одного и того же разреза графа

На рисунке 5.7: (а) Вершины множе-
ства S изображены чёрными. вершины из V \ S –белыми. Рёбра, пересекающие
разрез, соединяют белые вершины с чёрными. Единственное лёгкое ребро, пересекающее
разрез – ребро (d, с). Множество А состоит из серых рёбер. Разрез (S, V \ S) согласован
с А (ни одно ребро из А не пересекает разрез). (б) Вершины множества S изображены
слева, вершины V \ S – справа. Ребро пересекает разрез, если оно пересекает вертикальную
прямую.

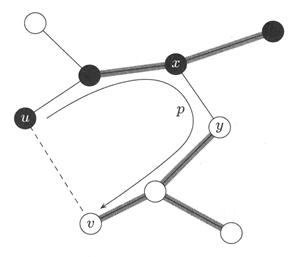
Рисунок 5.8 – К доказательству теоремы 5.8

На рисунке 5.8 все вершины S – чёрные, вершины V \ S – белые. Изображены только рёбра минимального остова (назовём его Т). Рёбра
множества А выделены серым цветом; (u, v) лёгкое ребро, пересекающее разрез (S, V \ S);
(х, у) – ребро единственного пути р от u к v в Т.

Остов Т связен и потому содержит некоторый (единственный) путь р из и
в v (рис. 5.8); ребро (и, v) замыкает этот путь в цикл. Поскольку вершины и и v
принадлежат разным частям разреза (S, V \ S), в пути р есть по крайней мере
одно ребро (х, у), пересекающее разрез. Это ребро не лежит в А, так как разрез согласован с А. Добавив к дереву Т ребро (и, v) и удалив из получившегося
цикла ребро (х, у), получим новый остов Т ' = Т \ {(х, у)} 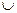{(u, v)}.

Покажем, что Т ' минимальный остов. Поскольку (и, v) – лёгкое ребро,
пересекающее разрез (S, V \ S), изъятое из Т ребро (х, у) имеет не меньший
вес, чем добавленное вместо него ребро (и, v), так что вес остова мог только
уменьшиться. Но остов был минимальным, значит, вес его остался прежним, и
новый остов Т ' будет другим минимальным остовом (того же веса). Поэтому
ребро (и, v), содержащееся в Т ', является безопасным.

Следствие 5.9. Пусть G = (V, Е) связный неориентированный граф и на мно-
жестве Е определена весовая функция w. Пусть А – множество рёбер графа,
являющееся подмножеством некоторого минимального остова. Рассмотрим лес
G _A = (V, А). Пусть дерево С – одна из связных компонент леса G _A. Рассмот-
рим все рёбра графа, соединящие вершины из С с вершинами не из С, и возьмём
среди них ребро наименьшего веса. Тогда это ребро безопасно для А.