2014-02-09
937
Непрерывная задача о рюкзаке
Дискретная задача о рюкзаке
Задача о выборе заявок
Жадные алгоритмы и динамическое программирование
Итак, что же представляют собой
жадные алгоритмы? Перед тем,
как ответить на этот вопрос, отве-
тим на другой: а что же есть алго-
ритм? Кажется, интуитивно мы это
понимаем, однако интуиция имеет
свойство подводить в самый не-
подходящий момент, причем очень
незаметно.
Просто алгоритмом будем назы-
вать механизм, который должен га-
рантировать не только то, что ре-
шение будет найдено, но и то, что
будет найдено именно оптималь-
ное решение. Кроме того, алго-
ритм должен обладать следующи-
ми качествами:
· Ограниченность по времени (работа алгоритма должна прекратиться за разумное время);
· Правильность (алгоритм должен находить правильное решение);
· Детерминистичность (сколько
бы раз не исполнялся алгоритм
с одинаковыми входными дан-
ными, результат должен быть
один и тот же);
· Конечность (описание работы алгоритма должно содержать
конечное число шагов);
· Однозначность (каждый шаг алгоритма должен интерпретироваться однозначно).
Эвристика
– это прямая противоположность
алгоритму, так как она не дает ни-
каких гарантий ни того, что реше-
ние будет найдено, ни того, что
оно будет оптимальным. Между
алгоритмом и эвристикой лежат
два понятия, которые называют
приблизительный алгоритм (ре-
шение гарантировано, но его оп-
тимальность – нет) и вероятност-
ный алгоритм (решение не гаран-
тировано, но если оно будет най-
дено, то будет обязательно опти-
мальным).
А теперь можно перейти к рас-
смотрению жадных алгоритмов.
Этот класс алгоритмов намного
проще и быстрее, чем динамиче-
ское программирование. Жад-
ный алгоритм делает на каждом
шаге локально оптимальный вы-
бор, надеясь, что итоговое решение окажется оптимальным. Од-
нако это не всегда так, и потому
иногда бывает, что жадный алго-
ритм в терминах вышеупомяну-
того определения – не полноцен-
ный алгоритм, а приблизитель-
ный. Но для большого числа ал-
горитмических задач жадные ал-
горитмы действительно дают оп-
тимум. Общую схему работы
жадных алгоритмов дадим в кон-
це, после рассмотрения конкрет-
ных примеров.
Пусть подано N заявок на прове-
дение занятий в одной и той же ау-
дитории. Для каждого занятия из-
вестно время его проведения
[ b i, e i], где b i – время начала заня-
тия, е i – время окончания. Два раз-
ных занятия не могут перекры-
ваться по времени, но условимся,
что начало одного может совпа-
дать с окончанием другого. Зада-
ча состоит в том, чтобы выбрать
максимальное число совместимых
по времени занятий.
Жадный алгоритм поступает так: упорядочим заявки в порядке воз-
растания времени окончания:
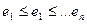. На сортировку понадобится време-
ни O (N × log(N)) в худшем случае.
Так как в этой статье проблема
сортировки не рассматривается,
положим, что массив уже отсорти-
рован по возрастанию. Далее все
предельно просто:
var
b,е: array[1..100] of integer;
{входные данные}
А: set of byte; {искомое множество}
i,j,n: integer;
begin
read(n);
for i:=1 to n do
read(b[i],e[i]);
А:= [1]; {начальное значение}
j:= 1; {самый правый отрезок множества А – первый}
for i:=2 to n do
if b[i]>=е[j] then begin
(если i-й отрезок лежит npaвee j-го)
А:=А+[i];
(то включаем j-й)
j:= i; (и запоминаем его как самый правый в множестве А)
end;
for i:=1 to n do (выводим результат)
if (i in А) then writeln(i);
end.
Листинг 5.21 – Задача о выборе заявок, рещаемая «жадным» алгоритмом
Вначале А содержит заяв-
ку j =1. Далее в цикле по i ищется
заявка, начинающаяся не рань-
ше, чем оканчивается заявка j.
Если таковая найдена, она вклю-
чается в множество А,и перемен-
ной j присваивается ее номер. Ал-
горитм требует всего лишь O (n)
шагов (без учета предваритель-
ной сортировки). Жадность этого
алгоритма состоит в том, что на
каждом шаге он делает выбор
так, чтобы остающееся свобод-
ным время было максимальным
(это и есть локально-оптималь-
ный выбор).
Теперь докажем, что этот алго-
ритм дает оптимальное решение.
Прежде всего, докажем, что суще-
ствует оптимальное решение за-
дачи о выборке заявок, содержа-
щее заявку 1 (с самым ранним
временем окончания). В самом
деле, если в каком-то оптималь-
ном множестве заявок заявка 1 не
содержится, то можно заменить в
нем заявку с самым ранним вре-
менем окончания на заявку 1, что
не повредит совместности заявок, (ибо заявка 1 кончается еще раньше, чем прежняя, и ни с чем пере-
сечься не может) и не изменит их
общего количества. Стало быть,
можно искать оптимальное мно-
жество заявок А среди содержащих заявку 1. После того, как мы
договорились рассматривать
только наборы, содержащие заяв-
ку 1, все несовместные с ней за-
явки можно выкинуть, и задача
сводится к выбору оптимального
набора заявок из множества ос-
тавшихся заявок (совместных с
заявкой 1). Другими словами, мы
свели задачу к аналогичной зада-
че с меньшим числом заявок. Pac
суждая по индукции, получаем,
что, делая на каждом шаге жад-
ный выбор, мы придем к опти-
мальному решению.
Вспомним динамическое про-
граммирование и попробуем ре-
шить ту же задачу с помощью не-
го. Заведем динамическую табли-
цу m [1.. n ], где m [ i ]означает мак-
симальное число совместных за-
явок среди набора с номерами
1.. i. Допустим, что подзадачи
m [1], m [2],..., m [ k -1] уже реше-
ны. Установим рекуррентную за-
висимость для решения задачи
m [ k ]: k -й отрезок можно брать, а
можно и не брать в искомое мно-
жество. Если мы его не берем, то
m [ k ] = m [ k -1], а если мы его бе-
рем, то
m [ k ] = 1 + m [ max(i такое, что e [ i ] ≤ s [ k ]) ]
Последнее выражение означает, что мы отбросили все заявки, не-
совместные с k‑й (левее нее), взя-
ли оптимум для оставшегося мно-
жества из динамической таблицы
плюс заявку k. Таким образом,
рекуррентная зависимость такова
m [ k ] = max{ m [ k -1], 1 + m [max(i та-
кое, что e [ i ] ≤ b [ k ]) ])
Для того, чтобы найти оптимальное множество (а не только количество
m [ n ] элементов в нем), надо завес-
ти дополнительный массив
рrеv [1.. n ], где prev [ k ] будет озна-
чать предыдущий элемент, (если
мы k -й брали), или -1 (если не бра-
ли k -й). Покажем, как выглядит ре-
ализация ДП-алгоритма, а потом
сделаем его оценку.
var
b,е,m,prev: array[0..100] of integer;
i,j,k,n: integer;
b
egin
read(n); for i:=1 to n do read(b[i],e[i]);
fillchar(prev, sizeof(prev), $FF);(заполняем -1)
m
[0]:= 0;
for k:=2 to n do begin
i:= k-1; (ищем i такое, что e[i]=b[k])
while (i>0) and (е[i] >b[k]) do dec(i);
if m[k-1] >= 1 + m[i] then
(если элемент лучше не брать)
m[k]:= m[k-1] (то не берем его)
else begin
m[k]:= 1 + m[i];
(иначе берем и)
prev[k]:= i; (запоминаем, что перед ним идет элемент i)
end;
end;
i:=n; (пробежимся с конца до начала и выведем все элементы)
repeat
if рrеv[i] =-1 then dec(i)
(если i-Й не брали, движемся дальше)
еlsе begin (в противном случае)
writeln(i); (выводим этот и)
i:= prev[i);
(перепрыгиваем через несовместимые слева от него)
end;
until i=0;
end.
Листинг 5.22 – Задача о выборе заявок, рещаемая ДП-алгоритмом
Даже не делая оценок сложности,
легко видеть, что ДП-алгоритм
сложнее жадного. Ну, а если быть
более точным, то его сложность
равняется O (n 2), так как существу-
ет два вложенных цикла (for по k и
внутренний while, который делает в с
реднем порядка O (n) сравнений и
уменьшений i). К тому же он требу-
ется порядка O (n) дополнительной
памяти. Таким образом, в этом слу-
чае жадный алгоритм намного эф-
фективнее динамического прог-
раммирования.
На складе есть N предметов, для
оторых известны их веса w [1.. N ] и их стоимости v [1.. М ]. На склад про-
брался вор, который хочет украсть
предметов на максимальную сум-
му денег. Однако вес, который вор
может вынести, ограничен и рав-
няется TotalW. Какие предметы
должен взять вор, чтобы их сум-
марная стоимость была наиболь-
шей, а вес был ограничен величи-
ной TotalW?
Эта задача встречается во многих
источниках, но часто ее решают
простым backtracking'ом, где на
каждом шаге пробуют взять или не
взять предмет. Однако такой под-
ход не всегда эффективен. Суще-
ствует как жадный, так и ДП-алго-
ритм ее решения.
Жадный алгоритм поступает так:
вычисляется цена единицы веса
каждого предмета, то есть рriсе [ i ]
:= v [ i ] / w [ i ]. Потом предметы сорти-
руются в порядке убывания
price [ i ], и вор начинает помещать в
свой рюкзак предметы по порядку
(i =1,2,... N) из отсортированного
списка. Если предмет i не помещается (по
ограничению оставшегося свобод-
ного веса в рюкзаке) - вор рассма
тривает следующий предмет 1+1
(price [ i + 1] < price [ i ]), и так до конца.
Жадность состоит в том, что вор
на каждом шаге пытается взять
предмет с наибольшей ценой.
Оценим сложность описанного алгоритма. Для сорти-
ровки надо O (N× log (N)) операций.
Далее надо пробежать циклом по i
от 1 до N и пробовать впихнуть
предмет i, таким образом это зай-
мет еще O (n) операций. Итого, об-
щая сложность есть O (N× log(N) +
N), что в общем случае эквива-
лентно O (N× log(N)).
Но если хорошо присмотреться, то
такой алгоритм не всегда дает оп-
тимум. Вот вам пример: 3 предме-
та, 1 - ($60, 10 кг), 2 - ($100, 20
кг), 3 - ($120, 30 кг) с ценами соот-
ветственно 6 $/кг, 5 $/кг, 4 $/кг.
Предметы уже отсортированы по
убыванию цены. Допустим, макси-
мальный вес рюкзака вора - 50 кг.
Следуя жадному алгоритму, вор берет первый предмет с ценой 6
$/кг, который весит 10 кг, затем
следующий предмет с ценой 5 $/кг
(и весом 20 кг), после чего в его
рюкзаке остается место только на
20 кг, и оставшийся предмет уже
не влезает, так как весит 30 кг.
Итого, действуя по жадному алго-
ритму, вор украл два предмета на
сумму $160 и весом 30 кг. Если бы
вор украл второй и третий предме-
ты (суммарным весом 50 кг), он бы
вынес $220. Как видите, жадный
алгоритм не дает оптимального
решения, а значит, он является
приблизительным алгоритмом.
Если решать эту же задачу с по-
мощью динамического програм-
мирования, то надо поступить
следующим образом. Допустим,
надо найти максимальную сумму
val [ W, i ], которую может вынести
вор, если допустить, что объем
его рюкзака не больше W и мож-
но брать предметы от 1 до i
(предметы не отсортированы!)
Допустим, мы уже нашли все
val [1.. W, 1.. i -1] (для веса не боль-
ше W и с возможностью брать
предметы от 1 до i -1). Рассмат-
ривается предмет i. Если его вес
w [ i ] меньше W, рассмотрим, сто-
ит ли его брать:
- Если его взять, то доступный вес в рюкзаке станет W - w [ i ] и мы
сможем забрать предметов на
сумму val [ W, i ] = val [ W - w [ i ], i -1]
+ v [ i ] (задача val [ W - w [ i ], i -1] уже
решена, плюс стоимость v [ i ] это-
го предмета); - Если его не брать, то доступный вес остается тем же, и тогда
val [ W, i ] = val [ W, i - 1].
Из этих двух вариантов выбирается тот, что дает большее значение
val [ W, i ]. Реализация ДП-алгорит-
ма будет выглядеть так:
const MAXW = 500; MAXN = 25;
var
val: array[0..MAXW,0..MAXN]of integer; (динамические массивы}
take: array[0.. MAXW,0..MAXN] of boolean;
v,w: array[1..MAXN] of integer;(ценности и веса предметов)
л, TotalW: integer; (кол. предметов,максимальный вес)
weight, i: integer;(переменные циклов}
begin
{читаем входные данные}
read(n, TotalW);
for i:=1 to n do read(w(i] v[i]);
(делаем начальную инициализацию для веса 0}
for i:=0 tо n dо begin
val[0,i]:= 0;
take[0,i]:= false;
end;
for weight:=1 to Totalw do val[weight 0]:= 0;
for weight:=1 to TotalW do
for i:= 1 to N do
if (w[i]>weight)
{если вещь не влезет}
{или лучше ее не брать}
or (val[weight, i-1] >= val [weight-w[i],i-l] i v[i))
then begin (то не берем ее)
val[weight,i]:=val[weight,i-1];
take[weight,i]:= false;
(отмечаем, что вещь i не взята)
end
else {иначе)
begin
{оптимум:= оптимум для веса weight-w[i] и использования
вещей 1..i-l + цена вещи i,
которую мы берем}
val [weight, i]:= val(weight-w[i],i-1] + v[i];
take[weight,i]:= true;
(отмечаем, что вещь i взята)
end;
(вывод результатов)
writeln('Best value:’, val[TotalW, N]);
write('Taken things; ');
weight:= TotalW;
for i:= N downto 1 do
if take[weight, i] then begin
write(i,' ');
weight:= weight - w[i];
end;
end.
Листинг 5.23 – Дискретная задача о рюкзаке, решаемая ДП-алгоритмом
Этот алгоритм будет выдавать
оптимальное решение, но какой
ценой? Ценой лишней памяти:
надо порядка O (TotalW × N) памяти
под динамические таблицы стои-
мости и запоминания того, брать
и каждый предмет или нет.
Сложность алгоритма та же: O
(TotalW× N), что следует из цик-
лов по weight и i.
Таким образом, ДП-алгоритм хоть и работает безупречно правильно,
но требует дополнительных затрат.
Есть, правда, еще одна проблема с
ДП-алгоритмом: если TotalW слиш-
ком велико, или же оно является
действительным (а не целым) чис-
лом, то ДП-алгоритм вообще не-
применим.
Условия те же самые, с той лишь
разницей, что предметы можно де-
лить на части, то есть вор может
украсть часть одного предмета. В такой задаче применим жад-
ный алгоритм, описанный выше (
с той лишь разницей, что если
очередной предмет из отсортиро-
ванного списка предметов не по-
мещается в рюкзак целиком, то о
т него вор берет ту часть, что п
омещается в рюкзак). Таким обр-
азом, если бы мы рассматривал-
и тот же пример из трех предмет-
ов 1 - ($60, 10 кг), 2 - ($100, 20 кг
), 3 - ($120, 30 кг), вор бы взял ц
еликом первый и второй из них; о
сталось свободным 20 кг в рюкз-
аке; вор отделил бы 2/3 части от т
ретьего предмета (что составит 20
кг) и забрал в сумме $60+$100 + 2/3*$120 = $240. Для непрерывной задачи о рюкзаке жадный алгоритм будет давать оптимальное решение.
Вычислить N чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, …, где первые два члена равны единице, а все остальные представляют собой сумму двух предыдущих, N меньше 100.
Самый очевидный способ «решения» задачи состоит в написании рекурсивной функции примерно следующего вида:
function F(X: integer): longint;
begin
if (X = 1) or (X = 2) then F:= 1
else F:= F(X-1) + F(X-2)
end;
Листинг 5.24 – Рекурсивная функция вычисления чисел Фибоначчи
При этом на шестом-седьмом десятке вызовов программе перестанет хватать временных ресурсов самой современной вычислительной машины. Это происходит по следующим причинам.
Для вычисления F(40) в начале вычисляется F(39) и F(38). Причем F(38) вычисляется заново, не используя значение, которое было вычислено, когда считалось F(39).
То есть значение функции при одном и том же значении аргумента считается много раз. Если исключить повторный счет, то функция станет заметно эффективней. Для этого приходится завести массив, в котором хранятся значения нашей функции:
var D: array[1..100] of longint;
Сперва массив заполняется значениями, которые заведомо не могут быть значениями функции (чаще всего, это «-1», но в вполне пригоден 0). При попытке вычислить какое-то значение, программа смотрит, не вычислялось ли оно ранее, и если да, то берет готовый результат.
Функция принимает следующий вид:
function F(X: integer): longint;
begin
if D[X] = 0 then
if (X=1) or (X=2) then D[X]:= 1
else D[X]:= F(X-1) + F(X-2);
F:= D[X];
end;
Листинг 5.25 – ДП-функция вычисления чисел Фибоначчи
Этот подход динамического программирования называется подходом «сверху вниз». Он запоминает решенные задачи, но очередность решения задач все равно контролирует рекурсия.
Можно еще более упростить решение, убрав рекурсию вообще. Для этого необходимо сменить нисходящую логику рассуждения (от того, что надо найти, к тривиальному) на восходящую (соответственно наоборот). В этой задаче такой переход очевиден и описывается простым циклом:
D[1]:= 1; D[2]:= 1;
For i:= 3 to N do
D[i]:= D[i-1] + D[i-2];
Листинг 5.26 – Итерационное вычисления чисел Фибоначчи
Здесь использован подход «снизу вверх». Чаще всего, такой способ раза в три быстрее. Однако в ряде случаев такой метод приводит к необходимости решать большее количество подзадач, нежели при рекурсии.
Очень часто для его написания приходится использовать как промежуточный результат нисходящую форму, а иногда безрекурсивная (итеративная) форма оказывается чрезвычайно сложной и малопонятной.
Таким образом, если алгоритм превышает отведенное ему время на тестах большого объема, то необходимо осуществлять доработку этого алгоритма.
Динамическое программирование
применимо именно в случаях, ког-
да подзадачи не являются незави-
симыми или же их зависимость ус-
тановить очень трудно. Алгоритм,
основанный на динамическом про-
граммировании, решает каждую из
подзадач всего один раз и запоми-
нает ответы для подзадач в специ-
альной таблице. Если подзадача
встретится еще раз, решение мож-
но взять из таблицы.
Как правило, динамическое про-
граммирование применяется к за-
дачам оптимизации,то есть к та-
ким, для которых существует боль-
шое количество решений, но их ка-
чество определяется каким-либо
фактором или параметром. Зада-
ча состоит в том, чтобы найти из
всех возможных решений то, кото-
рое обеспечивает экстремум (мак-
симум или минимум) этого пара-
метра.
Алгоритм, основанный на динамическом программировании, строит-
ся следующим образом:
1. Описывается строение оптимального решения;
2. Строится рекуррентное соотношение, связывающее задачу с ее подзадачами;
3. Делается обход дерева подзадач и
вычисляем оптимальное значе-
ние искомого параметра для
каждой из них, запоминая эти
решения в таблице;
4. Строится оптимальное решение с использованием полученной информации.
