Локальные и глобальные оптимальные решения

Описанная ниже стратегия нередко приводит к оптимальному решению задачи:

1) Находится произвольное решение;

2) Для улучшения текущего решения применяется к нему какое-либо преобразование из некоторой заданной совокупности преобразований. Это улучшенное решение становится новым «текущим» решением.

3) Указанная процедура повторяется до тех пор, пока ни одно из преобразований в заданной их совокупности не позволит улучшить текущее решение.

Результирующее решение может, хотя и необязательно, оказаться оптимальным. В принципе, если «заданная совокупность преобразований» включает все преобразования, которые берут в качестве исходного одно решение и заменяют его каким-либо другим, процесс «улучшений» не закончится до тех пор, пока не получим оптимальное решение. Но в таком случае время выполнения пункта (2) окажется таким же, как и время, требующееся для анализа всех решений, поэтому описываемый подход в целом окажется достаточно бессмысленным.

Этот метод имеет смысл лишь в том случае, когда можно ограничить совокупность преобразований небольшим ее подмножеством, что дает возможность выполнить все преобразования за относительно короткое время: если «размер» задачи равняется n, то можно допустить O (n ²) или O (n ³) преобразований. Если совокупность преобразований невелика, естественно рассматривать решения, которые можно преобразовывать одно в другое за один шаг, как «близкие». Такие преобразования называются «локальными», а соответствующий метод называется локальным поиском.

Одной из задач, которую можно решить именно методом локального поиска, является задача нахождения минимального остовного дерева. Локальными преобразованиями являются такие преобразования, в ходе которых берется то или иное ребро, не относящееся к текущему остовному дереву, оно добавляется в это дерево (в результате должен получиться цикл), а затем убирается из этого цикла в точности одно ребро (предположительно, ребро с наивысшей стоимостью), чтобы образовалось новое дерево.

Время, которое занимает выполнение этого алгоритма на графе из n узлов и e ребер, зависит от количества требующихся улучшений решения. Одна лишь проверка того факта, что преобразования уже неприменимы, может занять О (n ∙ e) времени, поскольку для этого необходимо перебрать e ребер, а каждое из них может образовать цикл длиной примерно n. Таким образом, этот алгоритм несколько хуже, чем алгоритмы Прима и Крускала, однако он может служить примером получения оптимального решения на основе локального поиска.

Алгоритмы локального поиска проявляют себя с наилучшей стороны как эвристические алгоритмы для решения задач, точные решения которых требуют экспоненциальных затрат времени (относятся к классу EXPTIME). Общепринятый метод поиска состоит в следующем. Начать следует с ряда произвольных решений, применяя к каждому из них локальные преобразования до тех пор, пока не будет получено локально-оптимальное решение, то есть такое, которое не сможет улучшить ни одно преобразование. Как показывает рисунок 5.17, на основе большинства (или даже всех) произвольных начальных решений нередко будут получаться разные локально-оптимальные решения. Если повезет, одно из них окажется глобально-оптимальным, то есть лучше любого другого решения.

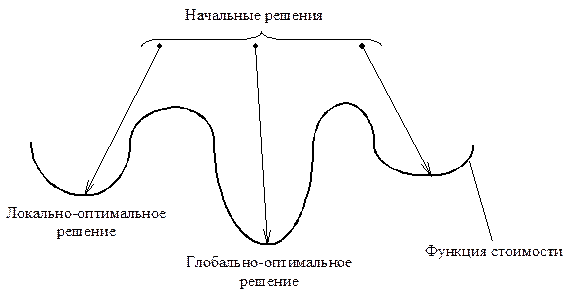
Рисунок 5.17 – Локальный поиск в пространстве решений

На практике можно и не найти глобально-оптимального решения, поскольку количество локально-оптимальных решений может оказаться колоссальным. Однако можно, по крайней мере, выбрать локально-оптимальное решение, имеющее минимальную стоимость среди всех найденных решений.

5.7 Метод декомпозиции («Разделяй и властвуй»)

Этот метод, называемый также методом «разделяй и властвуй» или методом разбиения, возможно, является самым важным и наиболее широко применимым методом проектирования эффективных алгоритмов. Он предполагает такую декомпозицию (разбиение) задачи размера n на более мелкие задачи, что на основе решений этих более мелких задач можно легко получить решение исходной задачи. В качестве примеров применений этого метода можно назвать сортировку слиянием или применение деревьев двоичного поиска, которые рассматриваются дальше. Иногда в литературе алгоритмами
с возвратом (backtracking algo-
rithms) называют все алгоритмы
полного перебора вглубь, а класс
более интеллектуальных, уменьшающих рост дерева поиска, выде-
ляют в подкласс алгоритмов вет-
вей и границ (branch and bound
algorithms). При использовании метода декомпозиции обычно применяется следующая последовательность действий:

1. Декомпозиция: разделяем задачу на k задач, меньших по раз-
меру (размером приблизительно
1 / k от исходной);

2. «Властвование»: процесс деле-
ния продолжаем рекурсивно до тех пор, пока полученные подза-
дачи не будут достаточно мало-
го размера для их тривиального
решения. Далее решаем полу-
чившиеся задачи.

3. Соединение: комбинируем решения подзадач в одно решение.

Важное условие: подзадачи, полу-
чившиеся в процессе разбиения,
не должны повторяться или частич-
но перекрывать друг друга. Если
условие не выполняется, то прин-
цип «разделяй и властвуй» к таким
задачам явно неприменим, и целе-
сообразнее использовать другие
методы.

5.7.1 «Ханойские башни»

Чтобы проиллюстрировать практическое применение принципа «разделяй и властвуй» рассмотрим хорошо известную головоломку «Ханойские башни». Имеются три стержня A, B и C. Вначале на стержень A нанизаны несколько дисков: диск наибольшего диаметра находится внизу, а выше – диски последовательно уменьшающегося диаметра. Цель головоломки – перемещать диски (по одному) со стержня на стержень так, чтобы диск большего диаметра никогда не размещался выше диска меньшего диаметра, и чтобы, в конце концов, все диски оказались нанизанными на стержень B. Стержень C можно использовать для временного хранения дисков.

Рисунок 5.16 – Головоломка «Ханойские башни»

Задачу перемещения n наименьших дисков со стержня A на стержень B можно представить себе состоящей из двух подзадач размера n -1. Сначала нужно переместить n -1 наименьших дисков со стержня A на стержень C, оставив на стержне A n -й наибольший диск. Затем этот диск нужно переместить с A на B. Потом следует переместить n -1 дисков со стержня C на стержень B. Это перемещение n - 1 дисков выполняется путем рекурсивного применения указанного метода. Поскольку диски, участвующие в перемещениях, по размеру меньше тех, которые в перемещении не участвуют, не нужно задумываться над тем, что находится под перемещаемыми дисками на стержнях A, B или C. Хотя фактическое перемещение отдельных дисков не столь очевидно, а моделирование вручную выполнить непросто из-за образования стеков рекурсивных вызовов, с концептуальной точки зрения этот алгоритм все же довольно прост для понимания и доказательства его правильности (а если говорить о быстроте разработки, то ему вообще нет равных). Именно легкость разработки алгоритмов по методу декомпозиции обусловила огромную популярность этого метода; к тому же, во многих случаях эти алгоритмы оказываются более эффективными, чем алгоритмы, разработанные традиционными методами.

var N: integer;

procedure MoveDisks(k: integer; X, Y, Z: char);

begin

if k=0 then exit; (выход из рекурсии)
MoveDisks(k-1, X, Z, Y); (подзадача 1)

writeln(X,' -> ',Y); (подзадача 2)
МоvеDisks(k-1, Z, Y, X);(подзадача 3)

end;

begin

read(N);

MoveDisks(N, 'А', 'В', 'С');

end.

Листинг 5.19 – Алгоритм решения задачи «Ханойские башни»

procedure Try(next_element);
begin

<включить next_element в искомое множество>;

if <достигнут нужный результат> then
begin

<запомнить этот результат> и/или

<вывести его на печать> и/или
<проверить на оптимальность>;

<выйти из процедуры, возможно
исключив next element

из этого множества>;

end;

<цикл перебора всех оставшихся или допустимых элементов
rest_element, который не обязательно должен быть
реализован в виде цикла for, while или repeat>
begin (в цикле)

<подсчет необходим локальных величин (*), если надо>;
if <условие обрезания дерева

перебора, которого может и не быть>

then Try(rest element);

<обратные действия к (*), если (*}
имели место>;

еnd;

<исключить пехt_е1еment из искомого множества»

end;

Листинг 5.20 – Обобщенный алгоритм решения задачи методом перебора