Алгоритм решения прямой задачи динамики при установившемся режиме движения машины

Решение задачи регулирования хода машины по методу Н.И.Мерцалова.

При расчете маховика (или решении задачи регулирования хода машины) по методу Н.И.Мерцалова задача решается в следующей последовательности:

• Определяются параметры динамической модели, например для ДВС М^пр_д - приведенный суммарный момент движущих сил и I^пр_II - приведенный момент инерции второй группы звеньев.
• Определяется работа движущих сил А_д интегрированием функции М^пр_д = f(j ₁) за цикл движения машины (допустим 2p);
• Определяется работа движущих сил за цикл и приравнивается к работе сил сопротивления А_д^ц = А_с^ц. Из этого равенства определяется среднеинтегральное значение момента сил сопротивления

М^пр_сср = А_с^ц/ (2p);

и для него строится диаграмма работы А_с = f(j ₁). Суммированием этой диаграммы и диаграммы А_д = f(j ₁) получаем диаграмму А = f(j ₁).

• Делается допущение w ₁» w _1ср, при котором T_II » I^пр_II *w _1ср²/ 2 (первое допущение метода Мерцалова), и определяется T_II = f(j ₁).
• Определяется кинетическая энергия первой группы звеньев

T_I = А -T_II + T_нач = А-T_II + T_Iнач + T_IIнач .

Так как начальные значения кинетической энергии неизвестны, то если учесть, что T_нач = T_Iнач + T_IIнач, D T_I = T_I - T_Iнач, D T_II = T_II - T_IIнач , получим

D T_I = А- _D T_II ,

то есть, вычитая из суммарной работы приращение кинетической энергии второй группы, получим приращение кинетической энергии первой группы.

По функции D T_I = f(j ₁) определяется максимальное изменение кинетиской энергии за цикл D T_Imax. Второй раз делаем допущение w ₁» w _1ср на основании которого, как показано выше, можно записать

I^пр_I = D T_Imax / (d *w _1ср²).

Из этого выражения, определив предварительно D T_Imax, можно решить две задачи:

• задачу синтеза - при заданном [d ] определить необходимый для его обеспечения приведенный момент инерции I^пр_{I нб} ,
• задачу анализа - при заданном I^пр_I определить обеспечиваемый им коэффициент неравномерности d.

Решение этой задачи рассмотрим на конкретном примере машинного агрегата привода буровой установки.

Дано: Кинематическая схема машины - l_AB = 0.12м, l_BC = 0.528м, l_BS2 = 0.169м, средняя частота вращения кривошипа - w _1ср = 47.124 рад/с², массы звеньев -

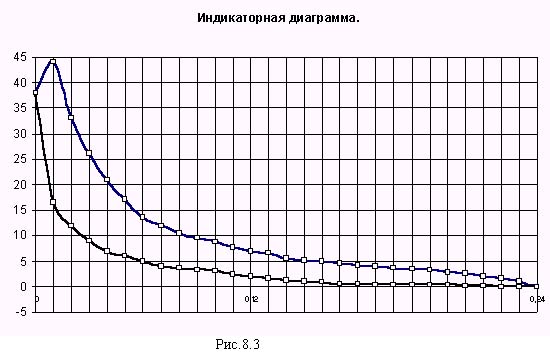
m₂ = 24.2 кг, m₃ = 36.2 кг, момент инерции - I _2S = 1.21 кг* м², I ₁₀ = 2.72 кг* м², максимальное давление в цилиндре - p_max = 4.4 МПа, коэффициент неравномерности вращения [d ] = 1/80, индикаторная диаграмма (приведена на рис. 8.3).

_________________________________________________________________

Определить: закон движения машины w ₁ = f(j ₁) и e ₁ = f(j ₁), момент инерции маховика I_доп , обеспечивающий заданную неравномерность вращения [d ].

1. Определение параметров динамической модели: М^пр_д - приведенного суммарного момента движущих сил и I^пр_II - приведенного момента инерции второй группы звеньев.
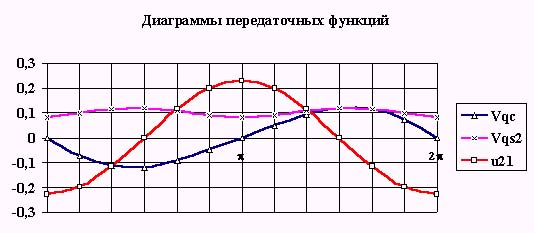
2. Определение первых кинематических передаточных функций. Определение кинематических передаточных функций для звеньев механизма u₂₁ = u₃₁ , центров масс V_qS1 , V_{qS2 и} V_qS3 и точки приложения движущей силы V_qD . Для определения этих функций воспользуемся методом проекций векторного контура механизма.

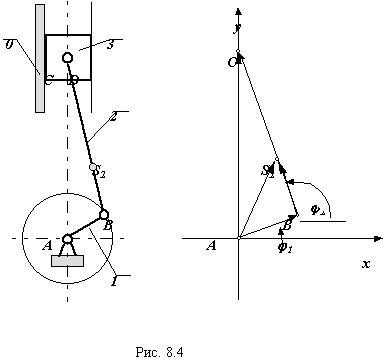
Рассмотрим следующие векторные контуры, изображенные на рис. 8.4 рядом со схемой механизма:

l _AB + l _CB = l _AC ; l _AS2 = l _AB + l _BS2 .

Для первого векторного контура l _AB+ l _CB = l _AC проекции на оси координат

l_AB * cos j ₁ + l_CB * cos j ₂ = x_C = 0,

l_AB * sin j ₁ + l_CB * sin j ₂ = y_C = S_C,

j ₂ = arccos (- l_AB * cos j ₁ / l_BC ).

Рис. 8.4

Производные от этих выражений

- l_AB * sin j ₁ - l_CB * u₂₁* sin j ₂ = 0,

l_AB * cos j ₁ + l_CB * u₂₁* cos j ₂ = V_qC ,

позволяют определить первые передаточные функции

u₂₁ = - l_AB * sin j ₁ / (l_CB* sin j ₂ ),

V_qC = l_AB * cos j ₁ + l_CB * u₂₁* cos j ₂ .

Для третьего векторного контура l _AS2 = l _AB + l _BS2 проекции на оси координат

x_S2 = l_AB * cos j ₁ + l_BS2 * cos j ₂ ,

y_S2 = l_AB * sin j ₁ + l_BS2 * sin j ₂ .

Производные от этих выражений

V_qS2x = - l_AB * sin j ₁ - l_BS2 * u₂₁* sin j ₂ ,

V_qS2y = l_AB * cos j ₁ + l_BS2 * u₂₁* cos j ₂,

позволяют определить первую передаточную функцию

Рис. 8.5

1.2. Определение приведенного момента движущих сил М^пр_д .

Индикаторную диаграмму (рис.8.3) строим по заданным значениям давления в цилиндре двигателя. Отрезок хода поршня Н_C* m _i делим на 10 интервалов. В каждой точке деления строим ординату диаграммы, задавшись (при p_i /p_max = 1) максимальной ординатой y_pmax. Тогда текущее значение ординаты

y_pi= y_pmax * (p_i/p_max ),

где p_max= 4.4 МПа.

Масштаб индикаторной диаграммы

m _p = y_pmax /p_max.

Площадь поршня S_п = p *d_п² /4.

При построении графика силы, действующей на поршень, ординаты этого графика принимаем равными ординатам индикаторной диаграммы. Тогда масштаб силы

m _F = m _p/S_п.

Для исследуемого механизма приведенный суммарной момент состоит из двух составляющих: движущей силы и момента сил сопротивления

M^пр = M^пр_д + M^пр_с.

Приведенный момент движущей силы определяется в текущем положении механизма по формуле

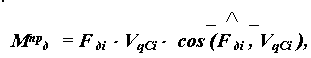
где F _дi - значение движущей силы,

F _дi = y_Fдi / m _F,

где y_Fдi - ордината силы сопротивления,

m _F - масштаб диаграммы сил.

V_qСi - значение передаточной функции в рассматриваемом положении механизма,

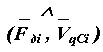
- угол между вектором силы и вектором скорости точки ее приложения.

Масштаб диаграммы по оси абсцисс определяется по формуле

m j = b / 2*p,

где b - база диаграммы (отрезок оси абсцисс, который изображает цикл изменения обобщенной координаты).

1.3. Построение диаграммы приведенных моментов инерции I_v^пр = I _II^пр.

Инерционные характеристики звеньев механизма в его динамической модели представлены суммарным приведенным моментом инерции. При расчете эту характеристику динамической модели представляетсяв виде суммы двух составляющих переменной I_v^пр = I _II^пр и постоянной I_c^пр = I_I^пр. Первая определяется массами и моментами инерции звеньев, передаточные функции которых постоянны, вторые - массами и моментами инерции звеньев передаточные функции которых переменны.

Проведем расчет переменной части приведенного момента инерции I_v^пр = I _II^пр. Для рассматриваемого механизма во вторую группу звеньев входят звенья 2 и 3. Звено 3 совершает поступательное движение, звено 2 -плоское. Расчет переменной части приведенного момента проводится по следующим зависимостям:

I_v^пр = I _II^пр = I_2В^пр + I_2П^пр+ I₃^пр,

где

I_2П^пр = m ₂ * V_qS2², I_2В^пр = I_S2 * u₂₁², I₃^пр= m₃* V_qС²,

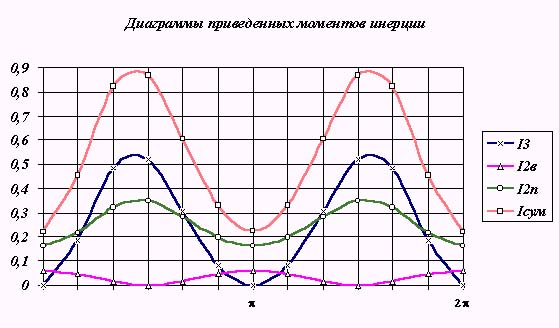
Рис. 8.7

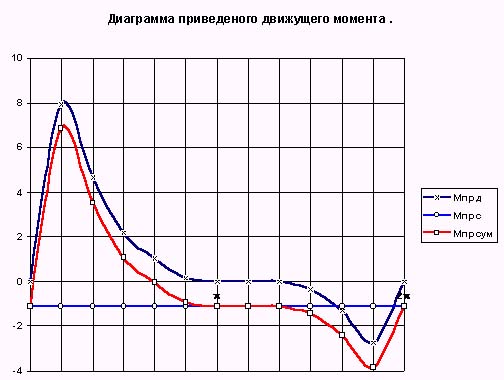
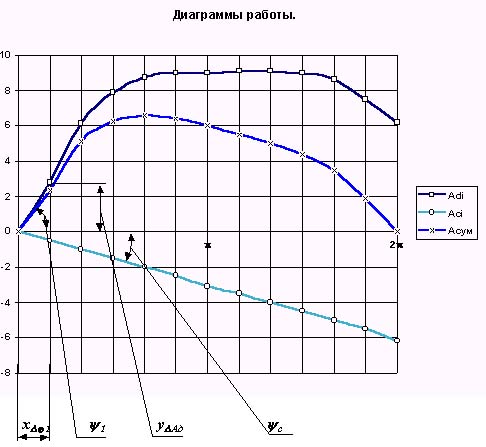
2. Построение диаграмм работы движущей силы, сил сопротивления и суммарной работы.

Диаграмму работы движущей силы получим интегрируя диаграмму ее приведенного момента

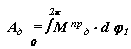
Интегрирование проведем графическим методом (рис.8.8), приняв при этом отрезок интегрирования равным k₁ . Тогда масштаб полученной диаграммы работы движущей силы будет равен

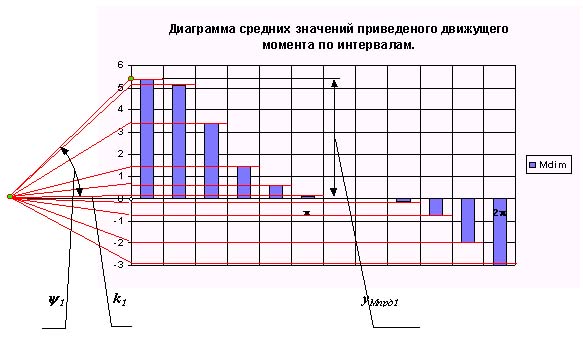
tg y ₁ = yD _Aд / xD j ₁ = y_Mпрд1/ k₁ D A_д * m _А/ (D j ₁ * m j) = M^пр _д1 * m _М / k₁

так как D A_д / D j ₁ = M^пр _д1, то m _А / m j = m _М / k₁, откуда

m _А = m _М *m j / k₁ .

Величина среднеинтегрального момента сил сопротивления определяется по формуле

М^пр_сср = А_с^ц/ (2p).

3. Построение диаграмм кинетических энергий.

Диаграммы кинетических энергий для первой и второй групп звеньев получает на основании теоремы об изменении кинетической энергии системы

D Т = Т - Т_нач, A = D Т _I + D Т _II .

График кинетической энергии второй группы звеньев получим из зависимости

Т _II = I_II ^пр*w _1ср² /2,

принимая, что w ₁» w _1ср. Тогда диаграмма приведенного момента инерции второй группы звеньев в масштабе рассчитанном по формуле

y_I = y_T I^пр_II * m _I = (I^пр_II * w _1ср² / 2) * m _T, откуда

m _T = 2* m _I /w _1ср²,

соответствует диаграмме кинетической энергии Т_II .

График кинетической энергии первой группы звеньев приближенно строим по уравнению

Т_I = Т - Т_II.

В каждом положении механизма из ординат кривой A= f (j ₁) вычитаем ординаты y_TII и получаем ординаты искомой диаграммы T_I = f (j ₁). Для этого необходимо ординаты диаграммы T_II = f (j ₁) из масштаба m _T перевести в масштаб m _A^* по формуле

y_TII^* = y_TII * m _A^*/ m _T.

Диаграмма кинетической энергии первой группы звеньев представлена на рис. 8.9.

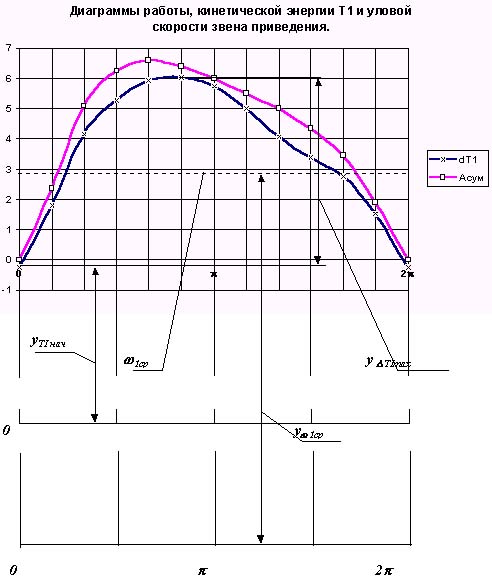
4. Определение необходимого момента инерции маховых масс первой группы

Максимальное изменение кинетической энергии звеньев перD вой группы за цикл определяем по диаграмме

D T_Imax = (y D _TImax )/ m _A.

Тогда необходимый момент инерции маховых масс первой группы звеньев, обеспечивающий заданный коэффициент неравномерности, равен

I_I^пр = D T_Imax / (w _1ср² * [d ] ).

4.1. Определение момента инерции дополнительной маховой массы.

В нашем случае момент инерции дополнительной маховой массы рассчитывается по следующей зависимости

I_доп = I_I^пр - I₁₀ ,

где I₁₀ - момент инерции коленчатого вала.

5. Построение приближенной диаграммы угловой скорости

Если считать, что w ₁» w _1ср, то

D T_I = I_I^пр*w _1ср * _{D w 1},

то есть диаграмма изменения кинетической энергии первой группы звеньев D T_I= f(j ₁) в другом масштабе соответствует диаграмме изменения угловой скорости D w ₁= f (j ₁). Если считать что ординаты диаграмм равны, то

yD w ₁ = yD _TI m _A* D T_I = m w * D w ₁ m _A* I_I^пр*w _1ср * _{D w 1} = m w * D w ₁ ,

откуда

m w = m _A* I_I^пр *w _1ср .

Ордината средней угловой скорости (для определения положения начала координат на диаграмме угловой скорости)

yw _1ср = w _1ср *m w.

После определения положения оси абсцисс на диаграмме угловой скорости можно определить начальное значение угловой скорости

w ₁₀ = yw ₁₀ /m w,

а по ней кинетическую энергию механизма в начальном положении

T_{I нач} = I_I^пр *w _1ср² /2.

6. Определение размеров маховика.

Принимаем конструктивное исполнение маховика - диск. Тогда его основные размеры и масса определятся по следующим зависимостям:

наружный диаметр

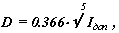
ширина b = y _b * D,

масса m = 1230* D ³,

где r = 7.8 кг/дм³ - плотность материала маховика,

y _b - коэффициент ширины.

7. Определение углового ускорения звена приведения.

Как отмечено ранее для расчета углового ускорения звена приведения e ₁ = f(j ₁) лучше пользоваться формулой:

e ₁ = dw ₁/dt = М ^пр/ I^пр- w ₁²/(2* I^пр) * (d I^пр /dj ₁).

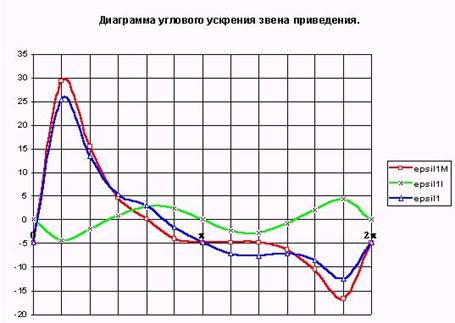
Необходимые для расчета значения величин определяем по ранее построенным диаграммам. Диаграмма функции e ₁ = f(j ₁ ) приведена на рис. 8.10.

Рис. 8.10