Комбинационные схемы. Как видно из рис. 1.2.9, устройство компьютера, преобразующее двоичную информацию, в общем случае, представляется многополюсником с n входами и m выходами

Как видно из рис. 1.2.9, устройство компьютера, преобразующее двоичную информацию, в общем случае, представляется многополюсником с n входами и m выходами. На его входы поступают входные двоичные сигналы x _i (i = 1..2,..., n), а с выхода снимаются выходные сигналы y_j (j = 1,2,..., m).

В любой момент времени наборы этих сигналов образуют соответственно входное слово X (x ₁, x ₂,..., x _n) и выходное слово Y (y ₁, y ₂,..., y _m).

Преобразование информации в компьютере производится логическими устройствами двух классов: комбинационными схемами и цифровыми автоматами.

В комбинационной схеме набор выходных сигналов (выходное слово Y) в любой момент времени полностью определяется набором входных сигналов (входным словом X), поступающих в тот же момент времени. Таким образом, в комбинационной схеме результат обработки данных зависит только от комбинации входных сигналов и вырабатывается одновременно с их поступлением.

Закон функционирования комбинационной схемы полностью определен, если задано соответствие между ее входными и выходными словами, например, в виде таблицы. По этой таблице можно получить аналитическую форму зависимости выходных и входных слов комбинационной схемы с использованием соответствующих логических функций.

Техническая реализация комбинационных схем производится логическими элементами, каждый из которых воспроизводит ту или иную логическую функцию двоичных переменных. Набор таких элементов должен обеспечивать реализацию функционально полной системы логических функций. В процессе синтеза логических устройств компьютера необходимо стремиться к минимальному числу и однородности используемых логических элементов.

Логические функции и соответствующие им комбинационные схе­мы подразделяют на регулярные и нерегулярные структуры.Регу­лярные структуры предполагают построение схемы таким образом, что каждый из ее выходов строится по аналогии с предыдущими выходами. В нерегулярных структурах такая аналогия отсутствует.

В качестве примера комбинационной схемы рассмотрим схему сравнения, или компаратор.

На вход компаратора поступают два двоичных числа A и B. Для каждого i-го разряда числа задаются три выхода:

1. 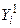, на который подается 1, если a_i > b_i и 0 – во всех остальных случаях.

2. 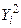, на который подается 1, если a_i = b_i и 0 – во всех остальных случаях.

3. 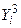, на который подается 1, если a_i < b_i и 0 – во всех остальных случаях.

Поскольку компаратор является регулярной структурой, т.е. схемы сравнения для каждого разряда числа идентичны, ограничимся построением функциональной схемы компаратора для одного разряда двоичных чисел A и B.

Таблица истинности для компаратора представлена в табл. 1.2.5.

Табл. 1.2.5. Таблица истинности для компаратора

По таблицам истинности можно определить аналитические выражения для выходов компаратора:

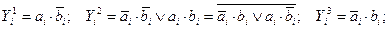
На рис. 1.2.12 показана функциональная схема компаратора.

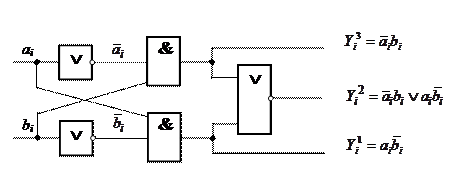
Рис. 1.2.12. Функциональная схема компаратора