Определение. Электрическим диполем называется система двух одинаковых по величине и противоположных по знаку зарядов 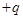 и
и 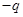 , расстояние
, расстояние 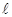 между которыми много меньше расстояния до тех точек, в которых определяется электрическое поле системы. Осью диполя называется прямая, проходящая через оба заряда.
между которыми много меньше расстояния до тех точек, в которых определяется электрическое поле системы. Осью диполя называется прямая, проходящая через оба заряда.
Потенциал поля системы зарядов 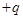 и
и 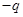 находится в любой точке в соответствии с (1.24) и рис. 1.13 как
находится в любой точке в соответствии с (1.24) и рис. 1.13 как
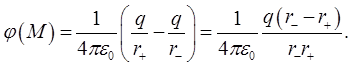 (1.35)
(1.35)
Так как 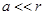 , то приближенно можно положить
, то приближенно можно положить
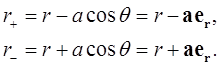 (1.36)
(1.36)
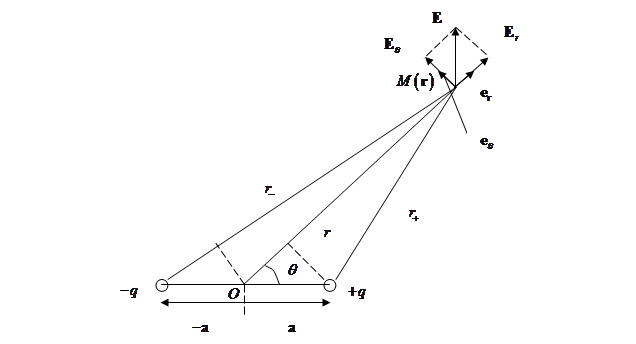
Рис. 1.13. К расчету электрического поля диполя,  ,
,
точка  - начало системы координат
- начало системы координат
Отсюда 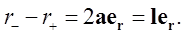 Кроме того, при
Кроме того, при 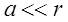 имеем:
имеем: 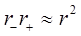 . Вместо (1.35) приближенно получаем
. Вместо (1.35) приближенно получаем
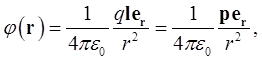 (1.37)
(1.37)
где 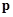 - электрический момент диполя,
- электрический момент диполя,
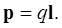 (1.38)
(1.38)
Вектор 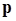 направлен вдоль оси диполя от отрицательного заряда к положительному (см. рис. 1.14).
направлен вдоль оси диполя от отрицательного заряда к положительному (см. рис. 1.14).

Рис. 1.14. Электрический момент диполя
Из (1.38) видно, что поле диполя определяется его электрическим моментом. Потенциал поля диполя убывает с расстоянием от него по закону 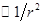 , то есть быстрее, чем потенциал точечного заряда (
, то есть быстрее, чем потенциал точечного заряда (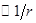 ). Поле диполя обладает осевой симметрией относительно оси диполя. Так как
). Поле диполя обладает осевой симметрией относительно оси диполя. Так как 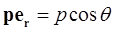 , то в полярной системе координат
, то в полярной системе координат 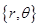 выражение (1.37) запишется как
выражение (1.37) запишется как
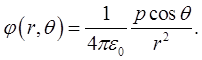 (1.39)
(1.39)
В полярной системе координат оператор «набла» записывается как
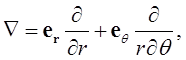 (1.40)
(1.40)
где 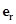 и
и 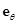 - базисные векторы данной системы координат (см. рис. 1.13).
- базисные векторы данной системы координат (см. рис. 1.13).
Подставим (1.40) в (1.33), получим выражение напряженности электрического поля диполя через потенциал в полярных координатах:
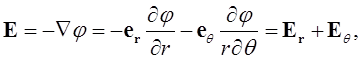 (1.41)
(1.41)
где с учетом (1.39)
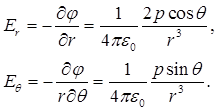 (1.42)
(1.42)
Модуль напряженности поля диполя
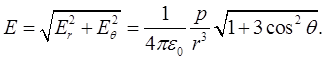 (1.43)
(1.43)
Напряженность поля диполя убывает с расстоянием от него по закону 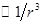 , то есть быстрее, чем напряженность поля точечного заряда (
, то есть быстрее, чем напряженность поля точечного заряда (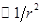 ).
).
Картина силовых линий электрического поля системы зарядов 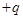 и
и 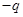 показана на рис. 1.15.
показана на рис. 1.15.
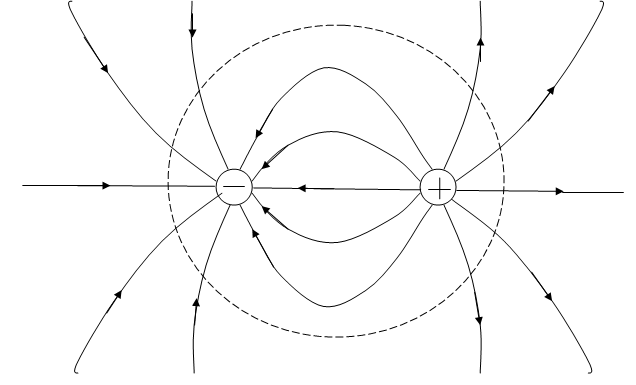
Рис. 1.15. Картина силовых линий электрического поля системы зарядов 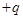 и
и 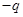 , формулы (1.40), (1.42) и (1.43) для поля диполя приближенно справедливы
, формулы (1.40), (1.42) и (1.43) для поля диполя приближенно справедливы
вне сферы (пунктирная линия) достаточно большого радиуса 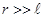 ,
,
где 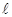 - расстояние между зарядами
- расстояние между зарядами
Плоскость 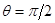 (перпендикулярна оси диполя и проходит через его середину) является эквипотенциальной:
(перпендикулярна оси диполя и проходит через его середину) является эквипотенциальной: 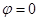 .
.
 2014-02-10
2014-02-10 10471
10471
