2014-02-10
1214
Принцип суперпозиции для сил электрического взаимодействия,
Пусть имеется система неподвижных электрических зарядов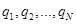 
и, кроме того, - неподвижный заряд 
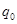(см. рис. 1.5).
Опыты показывают, что для сил электрического взаимодействия справедлив принцип суперпозиции: сила взаимодействия каждой пары зарядов не зависит от наличия других зарядов. Результирующая сила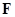 
, действующая на выделенный заряд 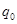со стороны остальных зарядов 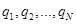, равна векторной сумме сил 
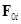, действующих на заряд 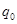со стороны каждого из зарядов 
, 
:
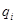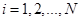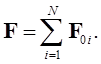(1.8)
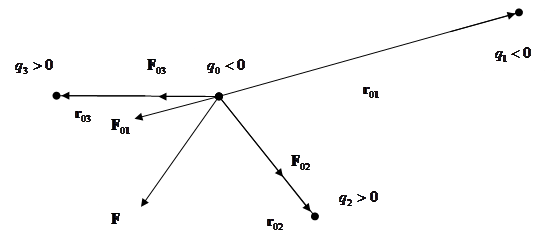
Рис. 1.5. К формулировке принципа суперпозиции
для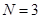 
, 
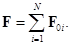
Используя принцип суперпозиции (1.7) и зная закон взаимодействия точечных зарядов (1.2), можно рассчитать силу взаимодействия между зарядами, сосредоточенными в телах конечных размеров, которые нельзя рассматривать как материальные точки. Пусть имеется два таких заряженных тела. Представим первое (второе) из них совокупностью большого числа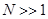 
(
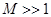) тел меньших размеров. Пусть каждую из составных частей в условиях решаемой задачи можно считать приближенно материальной точкой, но в то же время она содержит в своем составе большое число атомов и молекул. Каждую часть разбиения объемом 
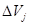в окрестности точки 
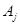с радиус-вектором 
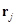можно рассматривать как точечный заряд некоторой величины 
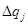, причем 
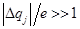. В силу последнего соотношения можно пренебречь флуктуациями величины заряда 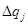из-за теплового движения заряженных частиц вещества.
Найдем полную силу электрического воздействия на тело 1 со стороны тела 2. Для этого по формуле (1.2) сначала найдем силу взаимодействия каждого выделенного точечного заряда тела 1 с каждым выделенным точечным зарядом тела 2. По принципу суперпозиции (1.7), полная сила, действующая на тело 1, равна векторной сумме всех сил, действующих на все точечные заряды тела 1 со стороны всех точечных зарядов тела 2. Далее, применяя третий закон Ньютона, можно выразить силу, действующую на тело 2 со стороны тела 1.
