Рассмотрим волну, распространяющуюся вдоль оси 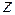 вид, который описывается функциями
вид, который описывается функциями

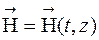 ,
,
это волны, имеющие плоский волновой фронт, так как фаза зависит только от Z
Из уравнения (3), для плоских волн соотношение
 ;
; .
.
Получим 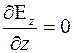 (
(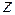 -я компонента вектора
-я компонента вектора 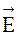 не зависит от координаты
не зависит от координаты 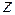 ).
).
Рассмотрим первое уравнение Максвелла для 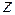 -ой компоненты
-ой компоненты
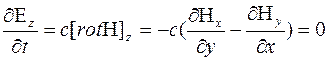
Выполнив аналогичные преобразования для всех компонент векторв 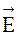 и
и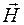 получаем следующие уравнения:
получаем следующие уравнения:
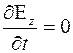
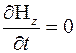 (5)
(5)
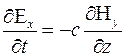
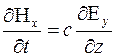 (6)
(6)
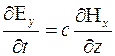
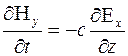 (7)
(7)
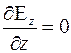
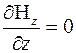 (8)
(8)
Уравнения показывают важнейшее свойство электромагнитных волн– их поперечность смотри 5 и 8.
Простейшей функцией, удовлетворяющей уравнениям Максвелла, является гармоническая волна
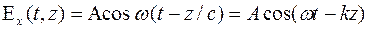 , (9)
, (9)
где 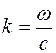 ,
, 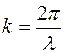 - модуль волнового вектора
- модуль волнового вектора 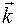 ,
,
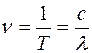 -частота колебаний,
-частота колебаний,
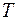 -период колебаний,
-период колебаний,
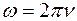 - круговая частата.
- круговая частата.
Направление волнового вектора 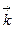 совпадает с направлением распространения волнового фронта (поверхности одинаковой фазы). Распространение волнового фронта описывается уравнением
совпадает с направлением распространения волнового фронта (поверхности одинаковой фазы). Распространение волнового фронта описывается уравнением
 .
.
Продифференцируем данное выражение по времени и найдем фазовую скорость:
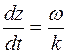 ;
; 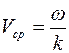
Проверим, удовлетворяет ли решение (9) волновому уравнению.
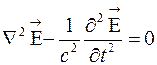
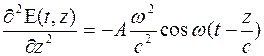
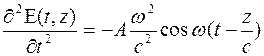
Функция (9) удовлетворяет волновому уравнению.
Найдем из уравнения Максвелла 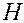 .
.
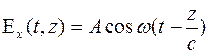
Воспользуемся уравнением Z.
 |
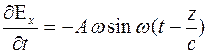
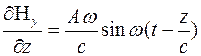
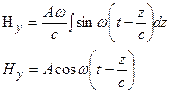
Вектора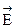 и
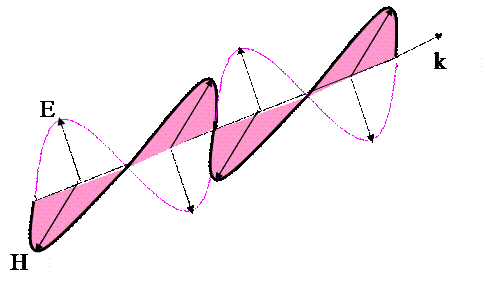
и 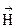 совершают в бегущей волне колебания в фазе, но в перпендикулярных плоскостях. (рисунок)
совершают в бегущей волне колебания в фазе, но в перпендикулярных плоскостях. (рисунок)
Если зафиксировать время t,то вдоль оси Z получим косинусоидальное-распределение напряженностей 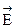 и
и 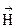 (мгновенная фотография).
(мгновенная фотография).
Если зафиксировать точку Z, то уравнения описывают изменение 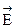 и
и 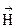 со временем.
со временем.
В общем виде можно записать уравнение волны, не зависящее от системы координат.
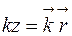
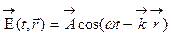 ,
,
здесь  радиус вектор, проведенный из начала координат в точку наблюдения.
радиус вектор, проведенный из начала координат в точку наблюдения.
Волновому уравнению удовлетворяют также волны
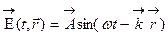
и волны, распространяющиеся в противоположном направлении.
 2014-02-10
2014-02-10 505
505







