Для описания распространения света в вакууме полагаем:
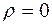 ,
, 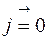 ,
,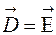 .
.
Система уравнений Максвелла в этом случае приобретает вид:
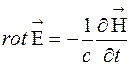 (1)
(1)
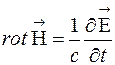 (2)
(2)
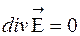 (3)
(3)
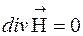 (4)
(4)
Найдем 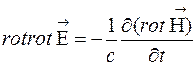 ,
,
с учетом уравнения (2) получим
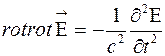
Используем соотношение 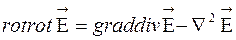 и с учетом уравнения (3) получим волновое уравнение для
и с учетом уравнения (3) получим волновое уравнение для 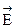 :
:
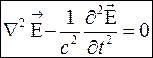
Аналогичное уравнение получается и для 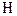 , для этого необходимо найти
, для этого необходимо найти 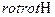 из уравнения (2)
из уравнения (2)
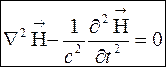
Так как вектора 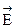 и
и 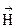 можно разложить по компонентам
можно разложить по компонентам
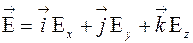
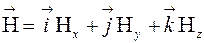 ,
,
то волновое уравнение для компонент примет вид
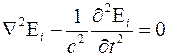 и
и
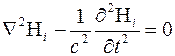 .
.
Иногда в этом случае говорят о скалярной волне. Рассмотрим скалярные волны, для этого вместо компонент векторов 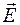 и
и 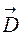 введена функция
введена функция 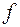
Решение волнового уравнения 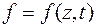 имеет в вид плоской волны, распространяющейся вдоль оси z, волновой фронт которой представляет собой плоскость перпендикулярную направлению распространения:
имеет в вид плоской волны, распространяющейся вдоль оси z, волновой фронт которой представляет собой плоскость перпендикулярную направлению распространения:
Волновое уравнение для данной функции:
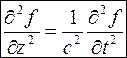
Решение определяется функцией вида 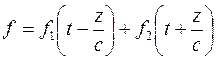 , это две бегущие волны, распространяющиеся в различных направлениях, в скобках записаны аргументы функций. Решение такого вида сохранят вид волны: это основное требование к волнам в вакууме. Проверим данное предположение. Найдем вид функции
, это две бегущие волны, распространяющиеся в различных направлениях, в скобках записаны аргументы функций. Решение такого вида сохранят вид волны: это основное требование к волнам в вакууме. Проверим данное предположение. Найдем вид функции 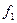 , которая описывает волну бегущую «вперед» в момент времени
, которая описывает волну бегущую «вперед» в момент времени 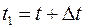 , учтем, что волновой фронт перемещается на расстояние
, учтем, что волновой фронт перемещается на расстояние 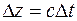 , тогда
, тогда
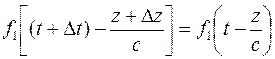 .
.
Аналогичные рассуждения для функции 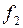 , которая описывает волну, бегущую «назад» дают равенство
, которая описывает волну, бегущую «назад» дают равенство
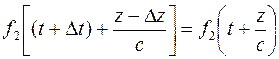 .
.
Решение выражает фундаментальный факт конечности скорости распространения электромагнитной волны.
Волна приходит в точку с координатой 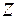 , через
, через 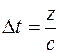 .
.
Обратите внимание, что в последующих курсах электродинамики все решения подобного вида носят название запаздывающих.
 2014-02-10
2014-02-10 1194
1194







