Рис. 2.5
Рис. 2.4
Эквивалентную схему катушки индуктивности представим в виде последовательно включенных индуктивности  и сопротивления
и сопротивления 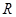 . Сопротивление
. Сопротивление 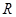 учитывает ряд факторов: омическое сопротивление провода, потери на перемагничивание сердечника, определяемые площадью петли гистерезиса, на вихревые токи за счет скин-эффекта и т.д. С ростом частоты потери, а значит, - и активное сопротивление
учитывает ряд факторов: омическое сопротивление провода, потери на перемагничивание сердечника, определяемые площадью петли гистерезиса, на вихревые токи за счет скин-эффекта и т.д. С ростом частоты потери, а значит, - и активное сопротивление 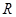 , растут. В результате изменяется и добротность катушки
, растут. В результате изменяется и добротность катушки 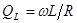 . Обычно на некоторой частоте величина
. Обычно на некоторой частоте величина 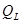 достигает максимума.
достигает максимума.
Перейдем к изучению нелинейных емкостей. Основной характеристикой нелинейной емкости служит вольткулонная характеристика 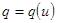 , где
, где 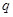 и
и 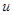 - заряд и напряжение на емкости. Зная вольткулонную характеристику, можно найти статическую емкость
- заряд и напряжение на емкости. Зная вольткулонную характеристику, можно найти статическую емкость
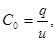 (2.13)
(2.13)
и дифференциальную емкость
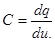 (2.14)
(2.14)
Ток через нелинейную емкость можно выразить как через 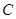 :
:
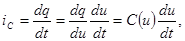 (2.15)
(2.15)
так и через 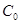 :
:
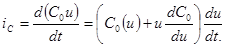 (2.16)
(2.16)
Обычно различают две группы устройств с нелинейной емкостью:
1) вариконды, нелинейность которых вызвана зависимостью диэлектрической проницаемости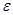 от напряженности электрического поля
от напряженности электрического поля 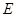 ;
;
2) варакторы или варикапы – полупроводниковые 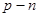 переходы, ширина запорного слоя которых, а значит, и расстояние между пластинами эквивалентного конденсатора зависят от приложенного напряжения.
переходы, ширина запорного слоя которых, а значит, и расстояние между пластинами эквивалентного конденсатора зависят от приложенного напряжения.
Зависимость индукции электрического поля 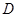 от
от 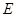 в варикондах имеет нелинейный характер. Для периодического изменения
в варикондах имеет нелинейный характер. Для периодического изменения 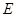 эта зависимость имеет вид петли гистерезиса (аналогично кривой намагничивания на рис. 2.4, а). Площадь петли определяет среднюю мощность потерь за период колебаний. С ростом частоты добротность
эта зависимость имеет вид петли гистерезиса (аналогично кривой намагничивания на рис. 2.4, а). Площадь петли определяет среднюю мощность потерь за период колебаний. С ростом частоты добротность 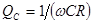 варикондов уменьшается. Поэтому они применяются лишь в низкочастотных схемах.
варикондов уменьшается. Поэтому они применяются лишь в низкочастотных схемах.
Перейдем к варакторам. В области отрицательных (обратных) напряжений  переход характеризуется зарядной или барьерной емкостью
переход характеризуется зарядной или барьерной емкостью 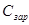 , зависимость которой от напряжения выражается как
, зависимость которой от напряжения выражается как
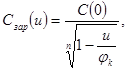 (2.17)
(2.17)
где 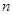 - параметр,
- параметр, 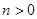 ,
, 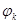 - контактная разность потенциалов. Величина
- контактная разность потенциалов. Величина 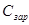 является дифференциальной емкостью. Для большинства варакторов
является дифференциальной емкостью. Для большинства варакторов 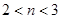 , причем резкому изменению концентрации доноров и акцепторов с обеих сторон
, причем резкому изменению концентрации доноров и акцепторов с обеих сторон 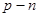 перехода соответствует
перехода соответствует 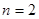 , а плавному -
, а плавному - 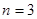 . Обычно при изменении обратного напряжения от нуля до напряжения пробоя
. Обычно при изменении обратного напряжения от нуля до напряжения пробоя 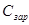 успевает измениться в
успевает измениться в 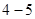 раз.
раз.
В области прямых напряжений 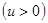 основной является уже не зарядная, а намного большая по величине диффузионная емкость
основной является уже не зарядная, а намного большая по величине диффузионная емкость 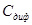 . Она настолько велика, что для ряда схем считают
. Она настолько велика, что для ряда схем считают 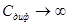 . Варакторы широко применяются для осуществления частотной модуляции, параметрического усиления колебаний, умножения и деления частоты, перестройки усилителей и генераторов.
. Варакторы широко применяются для осуществления частотной модуляции, параметрического усиления колебаний, умножения и деления частоты, перестройки усилителей и генераторов.
Подставив (2.17) в (2.14), найдем: 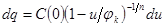 . Интегрируем это уравнение. Для определения константы интегрирования используем условие: при приложении прямого напряжения к диоду (варактору)
. Интегрируем это уравнение. Для определения константы интегрирования используем условие: при приложении прямого напряжения к диоду (варактору) 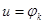 запорный слой исчезает, и тогда
запорный слой исчезает, и тогда 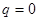 . Отсюда найдем вольткулонную характеристику варактора:
. Отсюда найдем вольткулонную характеристику варактора:
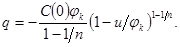 (2.18)
(2.18)
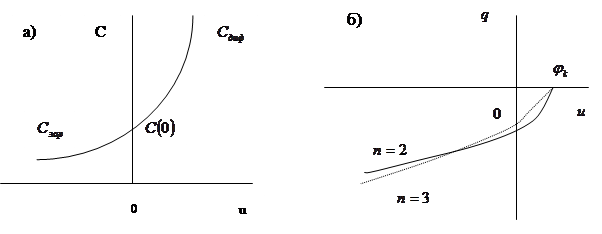
На рис. 2.5, а приведена характеристика варактора, а на рис. 2.5, б – его вольткулонная характеристика.
 |
На практике в качестве параметрических элементов обычно применяют нелинейные элементы, работающие в определенных условиях. Предположим, что на нелинейный элемент одновременно действует несколько входных сигналов: 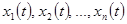 . В общем случае полный отклик можно представить как:
. В общем случае полный отклик можно представить как: 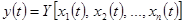 . В некоторых случаях отклик линейно зависит от одного из сигналов, например, - от
. В некоторых случаях отклик линейно зависит от одного из сигналов, например, - от 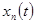 :
:
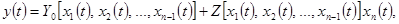 (2.19)
(2.19)
где 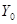 и
и 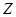 - некоторые нелинейные функции.
- некоторые нелинейные функции.
Тогда нелинейная система оказывается линейной параметрической: линейной, так как 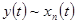 , и параметрической, так как параметр системы
, и параметрической, так как параметр системы 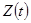 , определяющий влияние
, определяющий влияние 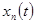 на
на 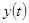 , зависит от времени
, зависит от времени 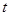 и не зависит от
и не зависит от 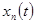 .
.
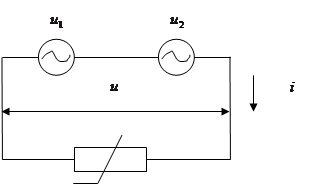
Пример. Пусть на нелинейный элемент (см. рис. 2.6) действует сумма гармонических колебаний:
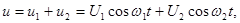 (2.20)
(2.20)
причем
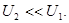 (2.21)
(2.21)
Условие (2.21) означает, что 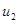 - небольшое отклонение от сильного сигнала
- небольшое отклонение от сильного сигнала  . ВАХ
. ВАХ 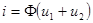 нелинейного элемента разложим в ряд Тейлора по степеням
нелинейного элемента разложим в ряд Тейлора по степеням 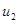 и ограничимся в разложении линейным приближением:
и ограничимся в разложении линейным приближением:
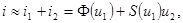 (2.22)
(2.22)
где 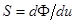 - крутизна характеристики, ток
- крутизна характеристики, ток  определяется лишь воздействием сильного сигнала
определяется лишь воздействием сильного сигнала  , ток
, ток 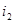 зависит от воздействия обоих сигналов
зависит от воздействия обоих сигналов  и
и 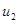 и определяется произведением меньшего из входных сигналов на дифференциальный параметр элемента – крутизну, управляемый сильным сигналом. Так как
и определяется произведением меньшего из входных сигналов на дифференциальный параметр элемента – крутизну, управляемый сильным сигналом. Так как  периодически изменяется с частотой
периодически изменяется с частотой 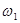 , то и крутизна
, то и крутизна 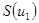 изменяется периодически с частотой
изменяется периодически с частотой 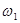 :
:
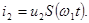 (2.23)
(2.23)
Зависимость (2.23) свойственна линейным (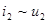 ) параметрическим (параметр
) параметрическим (параметр  зависит от времени) цепям.
зависит от времени) цепям.
 |
 2014-02-10
2014-02-10 545
545







