Статистические игры.
Статистические игры образуют специальный класс матричных игр, в которых одним из участников является человек или группа лиц, объединенных общностью цели (игрок А — статистик), а другим — «природа» (игрок П). Под термином «природа» подразумевается весь комплекс внешних условий, при которых статистику приходится принимать решение. Природа безразлична к выигрышу и не стремится обратить в свою пользу промахи статистика. Статистик может использовать m стратегий 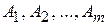 , природа может реализовать n различных состояний
, природа может реализовать n различных состояний 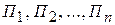 . Статистику могут быть известны вероятности
. Статистику могут быть известны вероятности 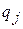 , с которыми природа реализует свои состояния
, с которыми природа реализует свои состояния 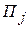 . Если статистик имеет возможность численно оценить (величиной
. Если статистик имеет возможность численно оценить (величиной 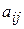 ) последствия применения каждой своей чистой стратегии
) последствия применения каждой своей чистой стратегии 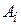 при любом состоянии
при любом состоянии 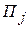 природы, то игру можно задать платежной матрицей (табл. 4.3). При упрощении платежной матрицы статистической игры имеется своя специфика: отбрасывать те или иные состояния природы (стратегии игрока П) нельзя, так как она может реализовать любое состояние независимо от того, выгодно оно статистику или нет.
природы, то игру можно задать платежной матрицей (табл. 4.3). При упрощении платежной матрицы статистической игры имеется своя специфика: отбрасывать те или иные состояния природы (стратегии игрока П) нельзя, так как она может реализовать любое состояние независимо от того, выгодно оно статистику или нет.
Таблица 4.3
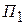 … … 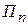
| 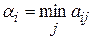
| |
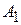 …
…
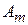
| 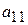 … … 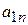 … … …
… … …
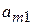 … … 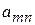
| 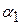 …
…
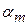
|
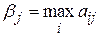
| 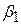 … … 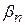
|
При выборе оптимальной стратегии статистика пользуются различными критериями. При этом опираются как на платежную матрицу, так и на матрицу рисков. Риском 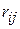 статистика, когда он пользуется чистой стратегией
статистика, когда он пользуется чистой стратегией 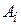 при состоянии природы
при состоянии природы 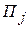 , называется разность между максимальным выигрышем
, называется разность между максимальным выигрышем 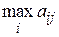 , который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние
, который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние 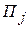 , и тем выигрышем
, и тем выигрышем 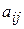 , который он получит, используя стратегию
, который он получит, используя стратегию 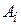 , не зная, какое же состояние
, не зная, какое же состояние 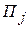 природа реализует. Таким образом, элементы
природа реализует. Таким образом, элементы 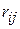 матрицы рисков (табл. 4.4) определяются по формуле
матрицы рисков (табл. 4.4) определяются по формуле 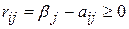 , где
, где 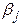 — максимально возможный выигрыш статистика при состоянии
— максимально возможный выигрыш статистика при состоянии 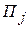 (максимальный элемент
(максимальный элемент 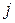 -го столбца платежной матрицы (табл. 4.3), т. е.
-го столбца платежной матрицы (табл. 4.3), т. е. 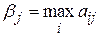 ).
).
Таблица 4.4
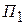 … … 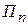
| 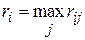
| |
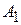 …
…
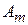
| 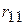 … … 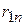 … … …
… … …
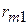 … … 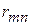
| 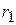 …
…
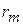
|
Если вероятности 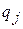 состояний природы
состояний природы 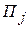 известны, то пользуются критериями Байеса и Лапласа. В качестве оптимальной по критерию Байеса принимается чистая стратегия
известны, то пользуются критериями Байеса и Лапласа. В качестве оптимальной по критерию Байеса принимается чистая стратегия 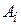 , при которой максимизируется средний выигрыш
, при которой максимизируется средний выигрыш 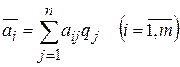 статистика, т.е. обеспечивается
статистика, т.е. обеспечивается
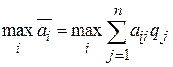 .
.
Если статистику представляются в равной мере правдоподобными все состояния природы 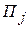 , то
, то 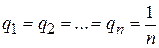 и оптимальной по критерию Лапласа считается чистая стратегия
и оптимальной по критерию Лапласа считается чистая стратегия 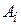 , обеспечивающая
, обеспечивающая
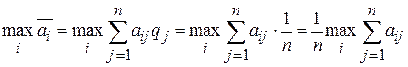 .
.
Если вероятности 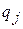 состояний природы
состояний природы 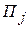 неизвестны, то пользуются критериями Вальда, Сэвиджа, Гурвица.
неизвестны, то пользуются критериями Вальда, Сэвиджа, Гурвица.
Оптимальной по критерию Вальда считается чистая стратегия 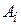 , при которой наименьший выигрыш статистика
, при которой наименьший выигрыш статистика 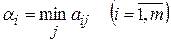 будет максимальным, т.е. ему обеспечивается
будет максимальным, т.е. ему обеспечивается
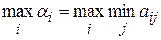 .
.
Оптимальной по критерию Сэвиджа считается та чистая стратегия 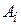 , при которой минимизируется величина максимального риска
, при которой минимизируется величина максимального риска 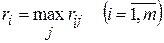 , т.е. обеспечивается
, т.е. обеспечивается
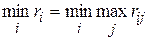 .
.
Оптимальной по критерию Гурвица считается чистая стратегия 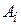 , при которой максимизируется величина
, при которой максимизируется величина 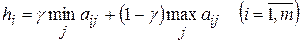 , т.е. обеспечивается
, т.е. обеспечивается
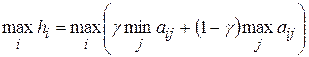 ,
,
где 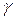 принадлежит интервалу (0; 1) и выбирается из субъективных соображений.
принадлежит интервалу (0; 1) и выбирается из субъективных соображений.
Анализ практических ситуаций проводится по нескольким критериям одновременно, что позволяет глубже исследовать суть явления и выбрать наиболее обоснованное решение.
Пример. За некоторый промежуток времени потребление основного вида топлива (мазута) на ТЭЦ в зависимости от качества составляет 18, 20 или 22 весовых единиц. Мазут можно закупить по оптовой цене, равной 7 ден. ед. за весовую единицу мазута. Если для обеспечения заданной температуры теплоносителя объема приобретенного мазута окажется недостаточно, то можно закупить недостающее количество мазута по розничной цене, равной 9 ден. ед. за весовую единицу мазута. Если же запас мазута превысит потребности, то дополнительные затраты на содержание и хранение остатка составят 3 ден. ед. в расчете на единицу веса мазута.
Требуется:
1) придать описанной ситуации игровую схему. Выявить участников игры и установить их характер. Указать допустимые стратегии сторон;
2) вычислить элементы платежной матрицы;
3) дать обоснованные рекомендации об уровне запаса мазута, при котором совокупные затраты на приобретение, содержание и хранение мазута будут минимальными при следующих предположениях:
а) вероятности потребности мазута в количестве 18, 20 и 22 весовых единиц известны и равны 0,2; 0,3 и 0,5. Найти оптимальную чистую стратегию, пользуясь критерием Байеса;
б) вероятности потребности мазута в количествах 18, 20 и 22 весовых единиц одинаковы. Найти оптимальную чистую стратегию, пользуясь критерием Лапласа;
в) о вероятностях потребления мазута в количествах 18, 20 и 22 весовых единиц ничего определенного сказать нельзя. Найти оптимальные чистые стратегии, пользуясь критериями Вальда, Сэвиджа, Гурвица (параметра 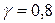 ).
).
 2014-02-10
2014-02-10 538
538








