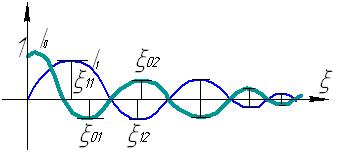
Амплитудно-частотная характеристика Фазово-частотная характеристика
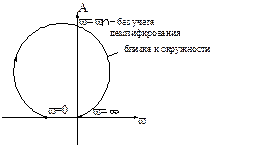
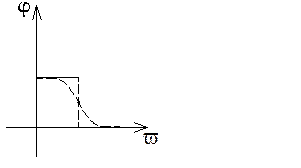
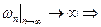 получается окружность
получается окружность
меньшего радиуса
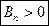 , т.е.
, т.е. 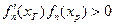
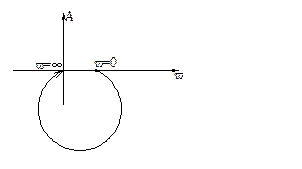
Т.к. есть рассеивание, то нет корней с положительной вещественной частью,  корни не дополняем.
корни не дополняем.
Не должно быть перемещений при A>0.
Для устойчивости не должно быть пересечений осей
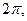
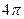 там где
там где 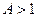 , иначе неустойчива (по критерию Найквиста).
, иначе неустойчива (по критерию Найквиста).
По каждому 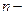 му тону получим, добавив АС
му тону получим, добавив АС
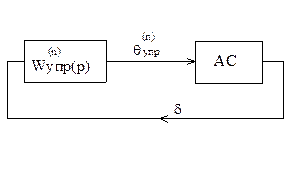
(первоочередными являются фазовые соотношения, т.к. амплитуда там максимальна)
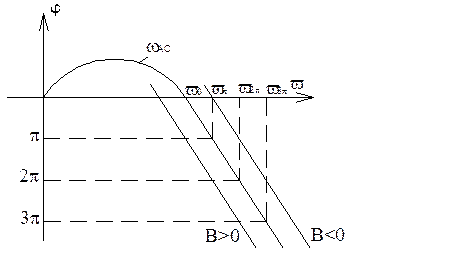
Если  , то
, то
если 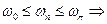 A>1
A>1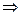 фазово-частотная характеристика пересекает ноль, а значит, система неустойчива.
фазово-частотная характеристика пересекает ноль, а значит, система неустойчива.
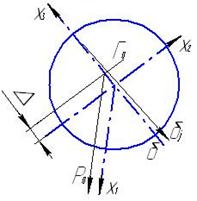
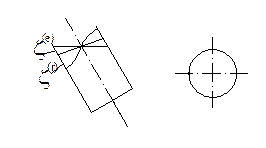
Диаграмма устойчивости объекта учитывает упругие колебания
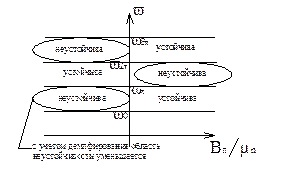
С помощью диаграммы, определим место положения гироскопов.
Лекция №4 (22.09.06.)
Задача 1. Есть АС, известны 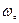 ,
, 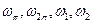 . Известны формы упругих колебаний
. Известны формы упругих колебаний 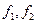 и место
и место
установки приборного отсека 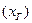 ,
, 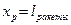 .
.
Определить устойчивость упругих колебаний.
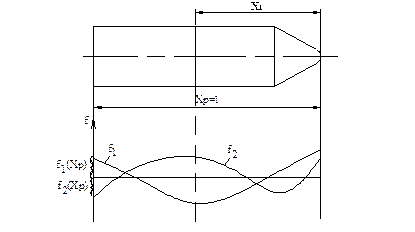
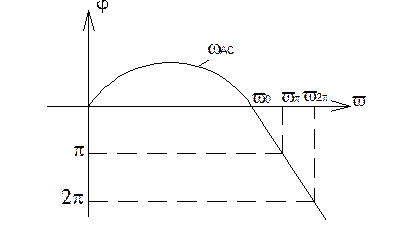
Пусть 
Построим производные
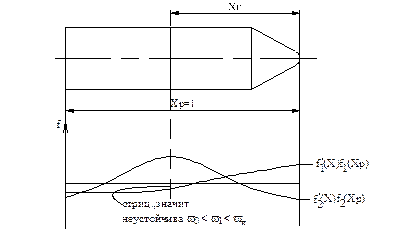
Задача 2. Выбрать место постановки гироскопа.
Дано: 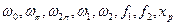
Найти: 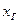
Пусть 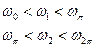
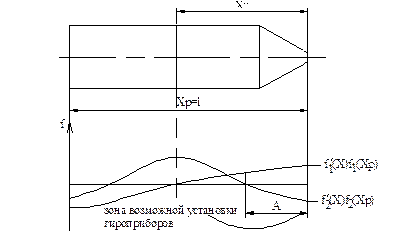
Задача 3. Формулировка требований к АС, где располагаются 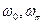 для устойчивости полета, т.е. подобрать параметры АС, если заданы все параметры:
для устойчивости полета, т.е. подобрать параметры АС, если заданы все параметры: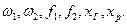
Определить 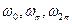
Пусть 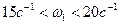 ;
; 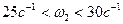 . Гироскоп расположен в передней части ракеты
. Гироскоп расположен в передней части ракеты 
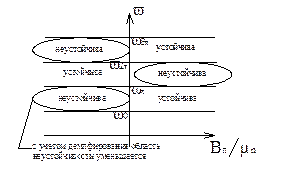
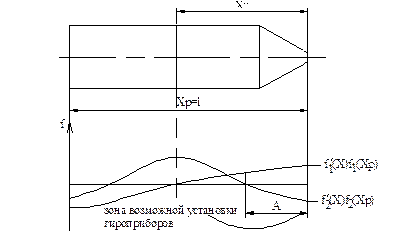 Можно сделать выводы:
Можно сделать выводы: 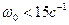
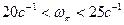
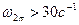 -фазовая стабилизация.
-фазовая стабилизация.
Стабилизацию упругих колебаний за счет изменения ФЧХ АС называют фазовой стабилизацией.
Задача 4. Есть 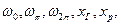 надо подобрать компоновку ракеты, т.е. определить
надо подобрать компоновку ракеты, т.е. определить 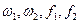
Задача 5. Выбор местоположения рулевого органа.
Есть 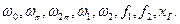
Определить 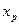
Пусть надо обеспечить стабилизацию по 3-м тонам (обычно по 3-м).
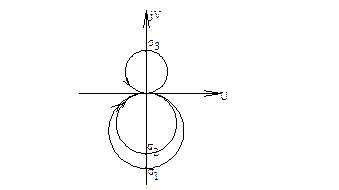
Ставим АС
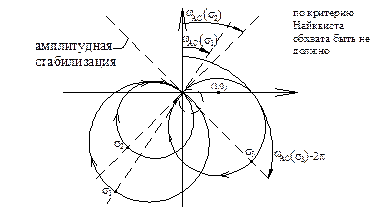
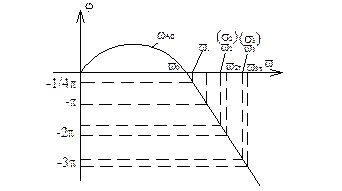
Если не удаётся стабилизировать все тона, то фазовостабилизируют только низшие тона, а для других используют амплитудную стабилизацию, (уменьшают радиус кольца).
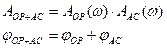
Методы амплитудной стабилизации:
1. Пассивный - не воздействуя на сам объект, гасят колебания.
1) Испытание постановкой фильтров, которые не пропускают сигналы на высших тонах, (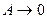 )
)
2) Использование датчиков угловых скоростей (ДУС) (лучше устанавливать в пучностях колебаний)
2. Активный - установка дополнительных устройств (т.е. переход к новой динамической системе), которые должны обеспечивать обратную связь и возбуждать колебания в противофазе возникшим упругим колебаниям (установка микродвигателей).
Могут возникнуть автоколебания  нарушение устойчивости как твердого тела.
нарушение устойчивости как твердого тела.
Метод начальных параметров
Рассмотрим модельную задачу.
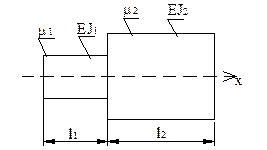
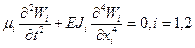 (1)
(1)
Граничные условия
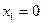
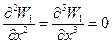
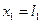
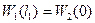
Условие стыковки
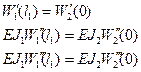
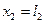
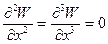
Решаем спектральную задачу.
Пусть 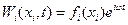 (2)
(2)
Тогда (1) с учетом (2) будет
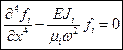 , где
, где 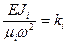
 Пусть
Пусть
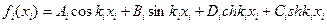
Из граничных условий
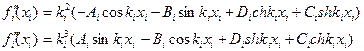
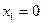
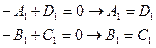
Из условий стыковки
Лекция №5. (29.09.06)
Основные соотношения и уравнения гидромеханики.
1. Теорема Коши-Гельмгольца:
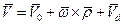 , где
, где 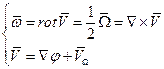
2. Уравнение неразрывности:
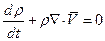
Примечание: большинство топлив – несжимаемые жидкости.
Для несжимаемых жидкостей:
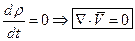 - однородная жидкость
- однородная жидкость
Для криогенных жидкостей:
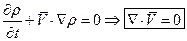 - неоднородная жидкость
- неоднородная жидкость
Для сжимаемых неоднородных жидкостей:
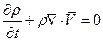
3. Уравнение движения:
Уравнение Эйлера (идеальная жидкость):
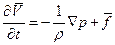
Уравнение Новье-Стокса: для вязкой жидкости:
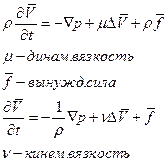
Уравнение сплошной среды:
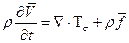
Примечание: для идеальной жидкости 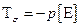 . В дальнейшем, будем считать жидкость идеальной.
. В дальнейшем, будем считать жидкость идеальной.
Тогда уравнение Эйлера:
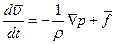
Если движение жидкости происходит в эллипсоидальном теле, то его движение подобно движению твердого тела относительно центра масс (вокруг неподвижной точки).
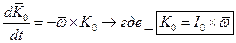
Примем 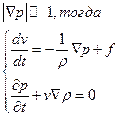
Что аналогично движению относительно неподвижной 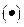 , не совпадающей с центром масс:
, не совпадающей с центром масс:
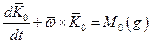
Т.е. можно использовать известные классические решения механики твердого тела.
Развернутое уравнение Эйлера:
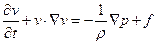
Допущения:
1) Баротропная жидкость: 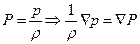 - функция давления
- функция давления
Можно считать, что перегрузка не зависит от х.
2) 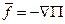
3) Безвихревое движение (во всем объеме): 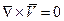 (
(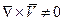 на поверхностях, близких к границам, т.е. поверхностям бака)
на поверхностях, близких к границам, т.е. поверхностям бака)
Интеграл Коши-Лагранжа:
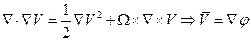
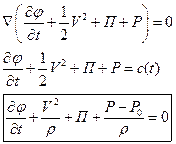 - интеграл Коши-Лагранжа
- интеграл Коши-Лагранжа
На свободной поверхности Г считаем:
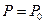 , т.е исключаем процессы газового переноса
, т.е исключаем процессы газового переноса 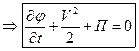 - на Г
- на Г
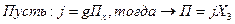
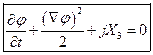 - на Г
- на Г 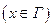 - динамическое условие
- динамическое условие
Ф(х,t)=0 – уравнение свободной поверхности Г: 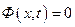
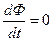
Или так как х – эйлерова координата:
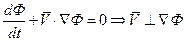
Решение уравнения с точностью до константы:
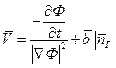
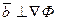 но он произволен
но он произволен
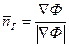
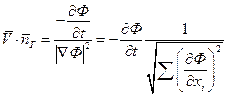
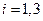
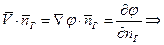
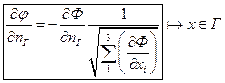 - кинематическое условие
- кинематическое условие
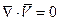 - условие неразрывности,
- условие неразрывности, 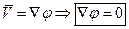 - уравнение Лапласа
- уравнение Лапласа
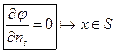 или
или 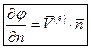
+Начальные условия: 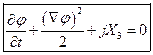
Постановка задачи:
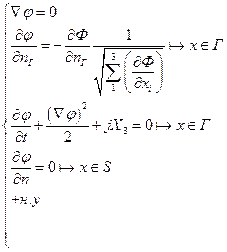
Линеаризация задачи:
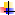 Отклонения жидкости малы, следовательно значениями квадратов их производных можно пренебречь:
Отклонения жидкости малы, следовательно значениями квадратов их производных можно пренебречь:
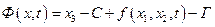
Для Г0: 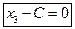 - уравнение свободной поверхности
- уравнение свободной поверхности
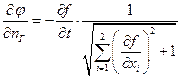
Возмущения относятся к поверхности Г0:
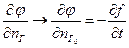
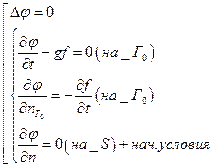 - линеаризованная постановка задачи
- линеаризованная постановка задачи
Пусть 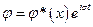
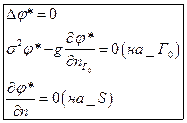 - спектральная задача
- спектральная задача
Пример:
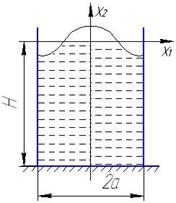
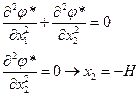
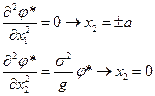
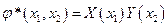
Получаем:
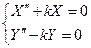
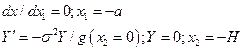
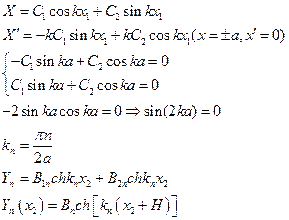
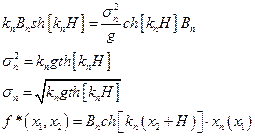
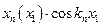 или
или 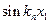
чётн. нечетн.
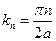
n=1 n=2
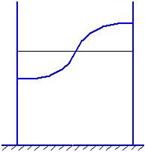
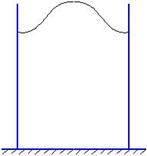
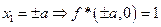
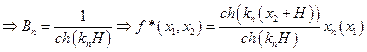
Решим эволюционную задачу:
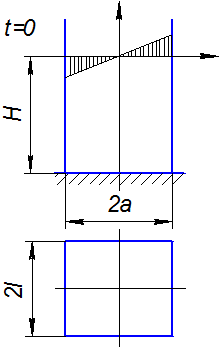
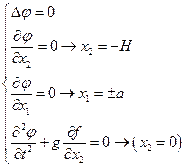
Введем поле смещений: 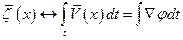
Обозначим потенциал смещения 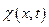 так, что в линеаризованной задаче
так, что в линеаризованной задаче 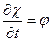
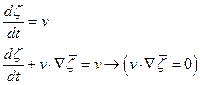
Переформулируем через потенциал смещений:
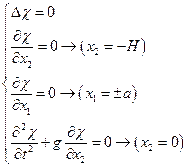
н.у.
t=0 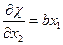 (a)
(a) 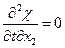 (б)
(б) 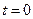
Найдем потенциал смещений виде:
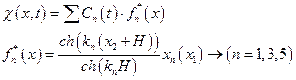
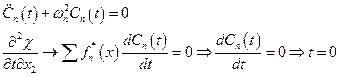
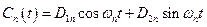
Так как 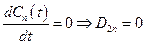
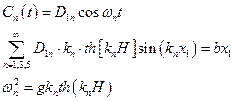
Разложим х1 в ряд по sin
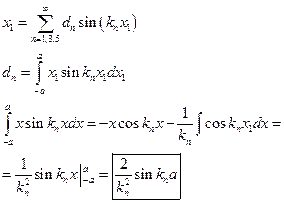
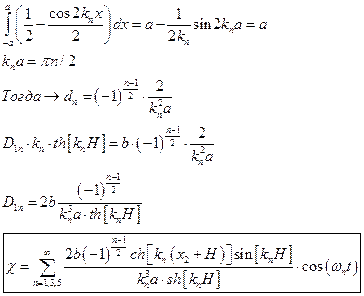
Допустим, что бак не подвижен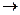 определим силу, воздействующую на боковую поверхность бака.
определим силу, воздействующую на боковую поверхность бака.
Лекция №6 (06.10.06):
Определим силу, воздействующую на боковую поверхность бака:
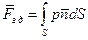 - главный вектор гидродинамических сил
- главный вектор гидродинамических сил
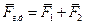 , где
, где 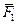 ,
, 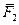 - проекции на ось
- проекции на ось
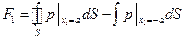
где 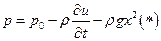
Так как 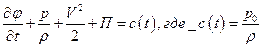
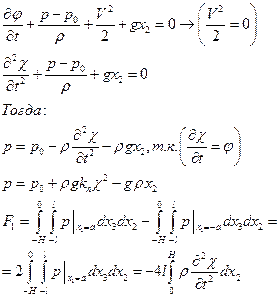
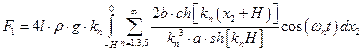
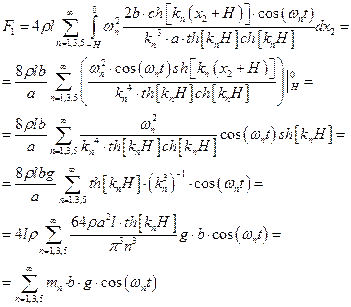
где 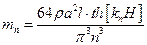 - приведенная масса колеблющейся жидкости
- приведенная масса колеблющейся жидкости
При 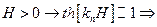
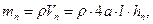
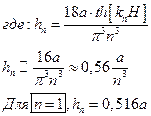
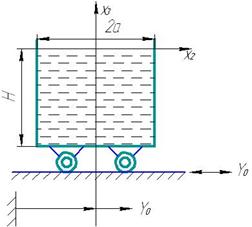
Волновое движение жидкости в круговом цилиндрическом баке:
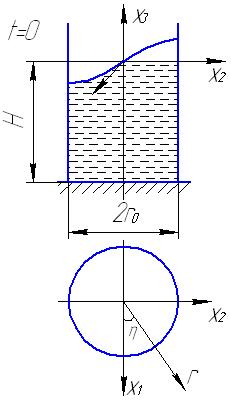
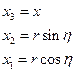
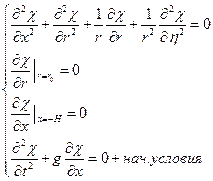
Пусть: 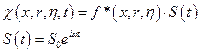
Рассмотрим спектральную задачу:
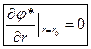
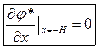
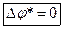
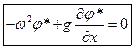
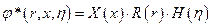
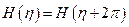
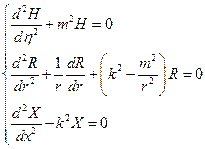
Условие периодичности:
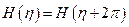
Тогда представим:
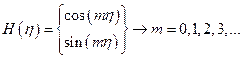
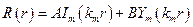
Можно положить В=0 (всплески в центре не рассматриваем)
Условия непротекания:
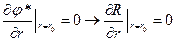
Тогда получим трансцендентное уравнение:
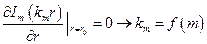
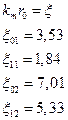
Тогда добавим индексы:
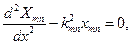
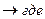
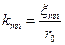
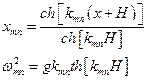
Решение:
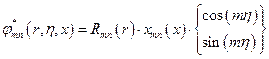
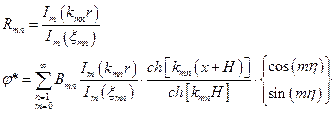
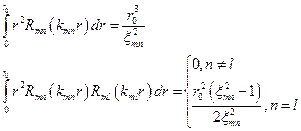
Задача – аналогична
Начальное отклонение: разложим в ряд
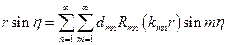 - ряд Фурье-Бесселя
- ряд Фурье-Бесселя
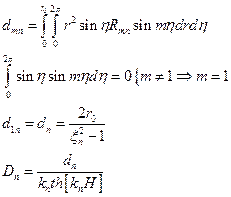
Решение – аналогично (в случае кругового цилиндра):
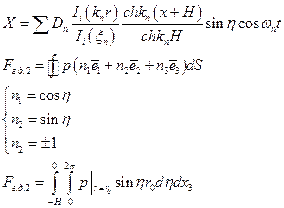
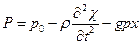
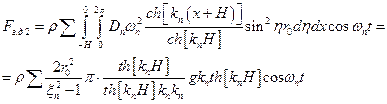
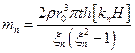 - приведенная масса (цилиндрический бак)
- приведенная масса (цилиндрический бак)
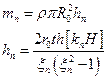
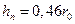 (точное значение
(точное значение 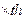 )
)
Формулировка задачи для потенциала скоростей и потенциала смещений в случае подвижной полости.
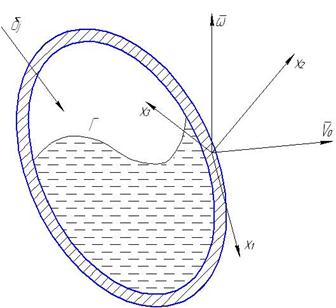
Уравнение поверхности: 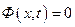
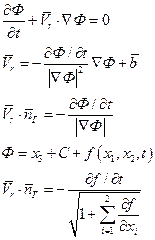
1) 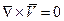
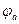 - потенциал абсолютной скорости
- потенциал абсолютной скорости
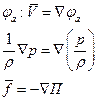
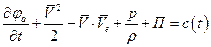
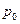 - давление газа
- давление газа
Тогда на Г:
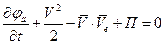 на Г – динамическое граничное условие
на Г – динамическое граничное условие
Формулировка задачи:
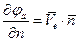 на S
на S
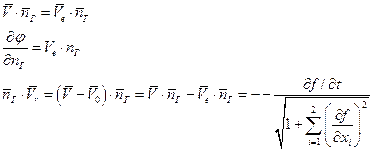
Тогда
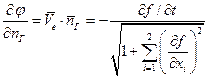
Окончательно:
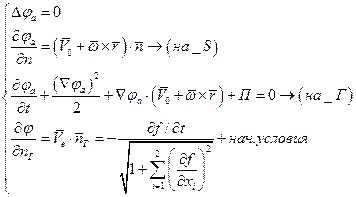
Лекция №7 (13.10.06):
Линеаризация задачи:
Движение жидкости и тела малые.
Тогда относительно неподвижной системы Oy1y2y3 поворот на углы 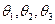 - поворот вокруг оси y1, y2, y3.
- поворот вокруг оси y1, y2, y3.
Тогда 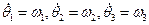 (в проекциях на Oх1х2х3)
(в проекциях на Oх1х2х3) углы малы.
углы малы.
Тогда 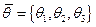
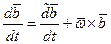 - формула Бура
- формула Бура
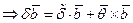
Введем вектор малых смещений: 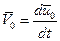
Примечание: 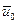 и
и 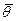 - малые величины
- малые величины
Введем потенциал смещений: 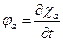
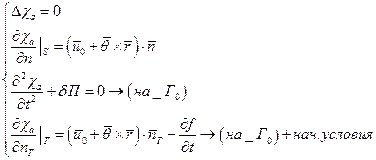
Если задать: 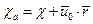 (избавляемся от u0)
(избавляемся от u0)
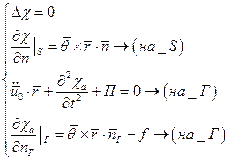
Зададим поступательное движение бака.
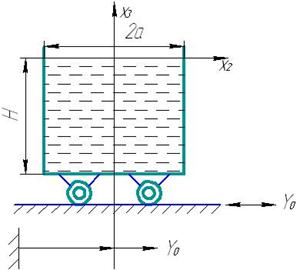
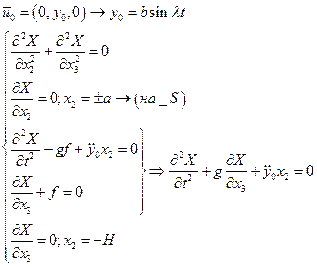
+ начальные условия
Пусть:
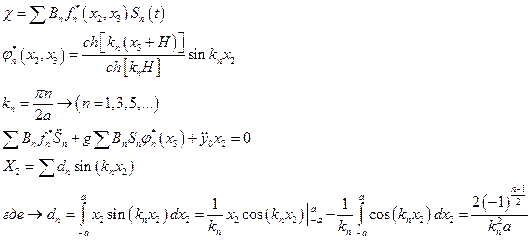
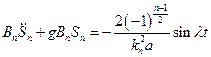
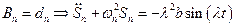
См. только вынужденные (уст-ся)
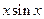
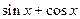
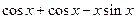
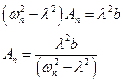
Всё решение запишется в виде:
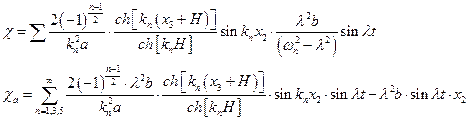
Сила, действующая на стенки баков:
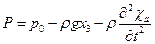
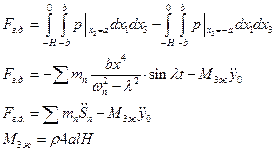
Движение бака с жидкостью:
Задано 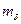
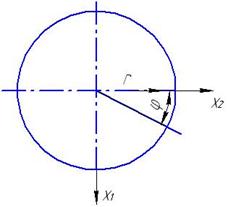
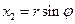
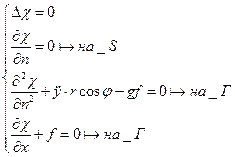
В полярных координатах:
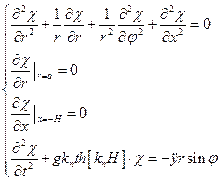
Пусть
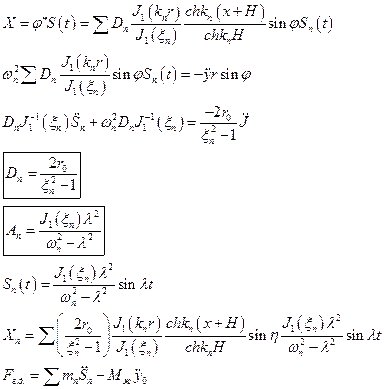
Вращательное движение бака.
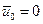
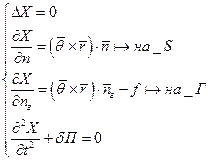
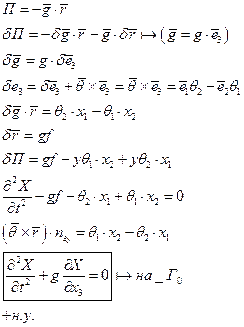
К поступательному движению:
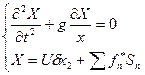 или
или 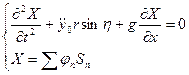
Тогда
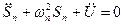
Лекция №8 (20.10.06)
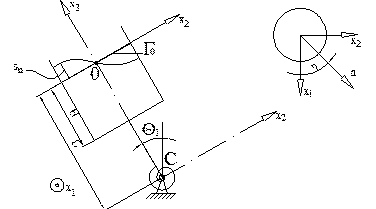
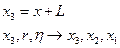
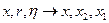
Постановка эволюционной задачи:
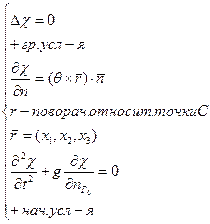
На S (1)
- условие свободной поверхности на Го (*)
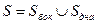
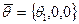
Из (1) распишем:
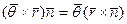 = (т.к. только
= (т.к. только 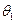 , то берем первые проекции)=
, то берем первые проекции)= 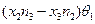

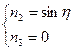 на
на 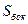 ;
; 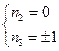 на
на 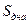 и
и 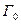
Запишем задачу в системе координат не связанной с поверхностью
Конкретная постановка задачи
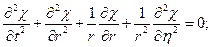
Условие на боковой поверхности:
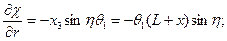
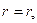 (2)
(2)
Условие на дне:
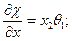
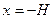 (3)
(3)
Условие на свободной поверхности:
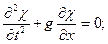 на
на 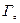 ,
,  (4)
(4)
+начальные условия
Решения будем искать в виде
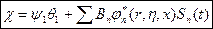 (5)
(5)
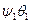 -от вращения, удовлетворяет равенствам с
-от вращения, удовлетворяет равенствам с 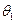 (если
(если 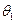 нет, то нет вращения)
нет, то нет вращения)
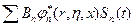 -обусловлено собственным колебанием жидкости (в
-обусловлено собственным колебанием жидкости (в
неподвижном баке со свободной поверхностью)
Потенциал 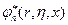 был определен в прошлых лекциях и имеет вид:
был определен в прошлых лекциях и имеет вид:
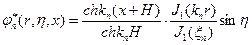

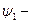 единичный потенциал, даёт описание вращения тела вокруг оси
единичный потенциал, даёт описание вращения тела вокруг оси 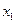 с единичной
с единичной
Скоростью
Для идеальной жидкости при линейной задаче действует принцип суперпозиции
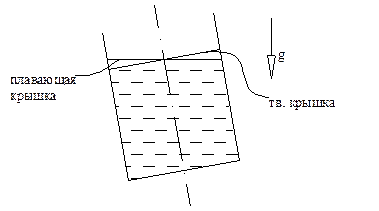 Пример краевой задачи с неоднородными граничными условиями
Пример краевой задачи с неоднородными граничными условиями
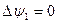
Подставляем в (2), получаем
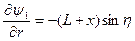 ,
, 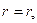
Подставляем в (3), получаем
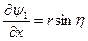 ;
; 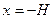
Подставляем в(4), получаем
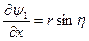
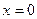
-считаем, что бак закрыт твердой крышкой
Найдем потенциал 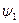
Пусть 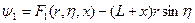 - описывает переносное движение
- описывает переносное движение
Задача для 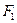
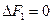 ; (6)
; (6)
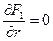 ;
; 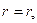
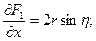
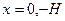 (7)
(7)
Разделяя переменные в (6), получим 3 уравнения
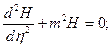 - отвечает
- отвечает 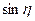 ,
,
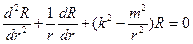 ;-отвечает
;-отвечает 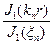
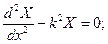
Нам удовлетворяет только 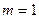 ,тогда структура потенциала
,тогда структура потенциала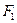 :
:
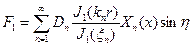 (8)
(8)
Подставляем в (7), получим
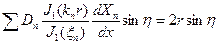
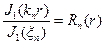
Разложим 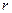 в ряд по функции
в ряд по функции 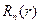
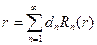 , где
, где 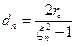 см. прошлую лекцию
см. прошлую лекцию
Положим, что 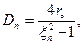 тогда
тогда
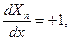
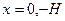
Решение для X будут гиперболические функции
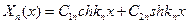 ;
; 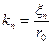
Найдем константы 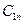 и
и 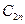
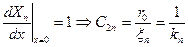
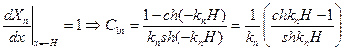
Т.к. 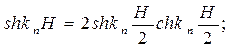
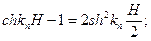
То 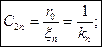
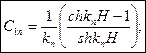
Тогда 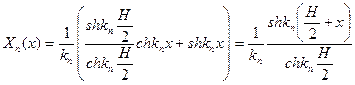
И 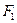 примет вид:
примет вид:
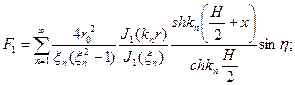
А потенциал 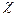 будет:
будет:
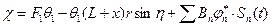 ;
;
Найденный потенциал должен удовлетворять условию на свободной поверхности. Подставим выражение для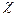 в уравнение со (*). Получим уравнение для обобщенной координаты.
в уравнение со (*). Получим уравнение для обобщенной координаты.
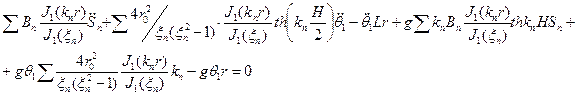
Разложим 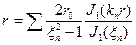
Тогда 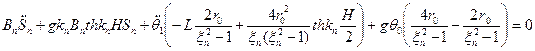
Выберем 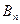 так, чтобы
так, чтобы 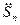 осталось с коэффициентом 1:
осталось с коэффициентом 1:
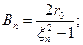
Тогда 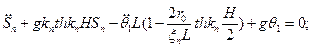
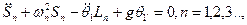
Где 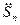 -обобщенная координата волнового движения жидкости.
-обобщенная координата волнового движения жидкости.
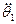 -обычно задано
-обычно задано
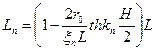 -приведенная длина.
-приведенная длина.
Найдем гидродинамическую силу:
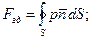
Гидродинамический момент относительно точки С:
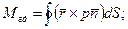
Найдем 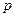 из интеграла Коши – Лагранжа:
из интеграла Коши – Лагранжа:
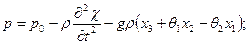
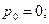
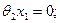
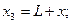
Распишем гидродинамическую силу:
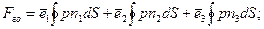
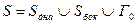
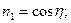
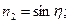
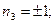
Тогда 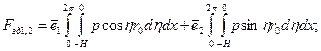
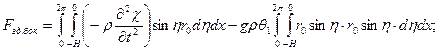
Где 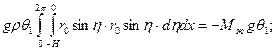
Напомним, 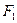 имеет вид:
имеет вид:
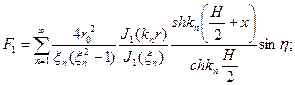
А потенциал 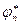 имел вид:
имел вид:
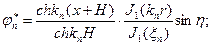
В данном случае 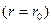
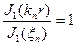
Обозначим интегралы:
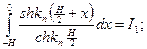
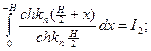
Вычислим эти интегралы:
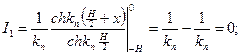
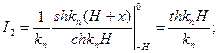
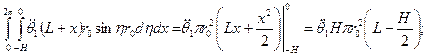 -свободный член в
-свободный член в 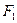
Лекция№9 (27.10.06)
Тогда 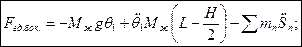
Где 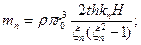 -приведенная масса колеблющейся жидкости.
-приведенная масса колеблющейся жидкости.
Определим моменты:
Гидродинамический момент относительно точки С
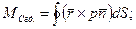
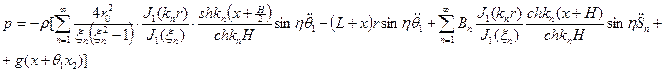 Вращение происходит только относительно оси
Вращение происходит только относительно оси 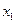 , тогда
, тогда
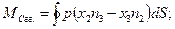
Пусть 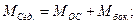 где
где 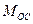 - момент относительно оси
- момент относительно оси
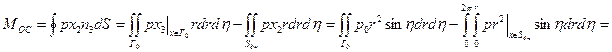
Т.к.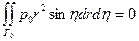 ,то
,то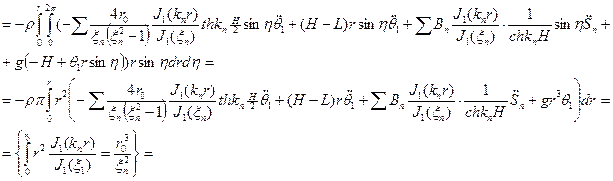
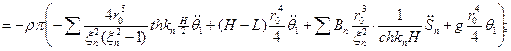
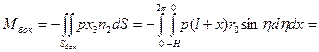
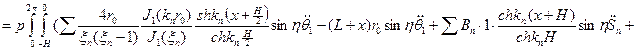
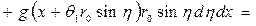
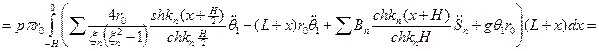
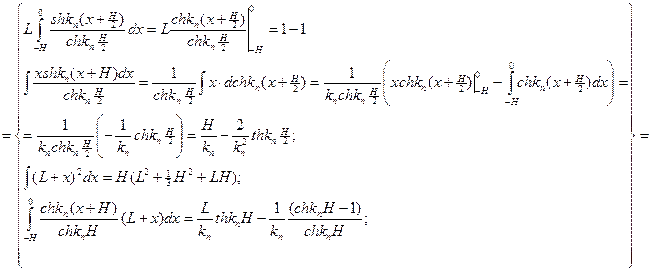
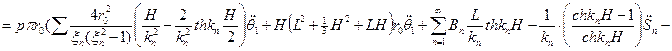
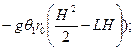
Т.к. 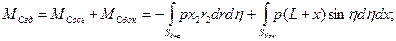
Т.к. 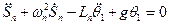
Где 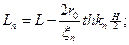
Из математики известно: 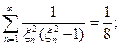
Тогда из (9) получим:
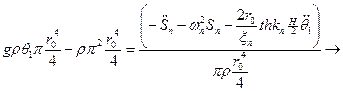 можно заменить на сумму
можно заменить на сумму 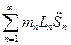
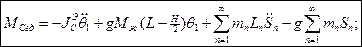
где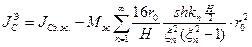 -эквивалентный момент инерции
-эквивалентный момент инерции
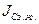 -момент инерции затвердевшей жидкости
-момент инерции затвердевшей жидкости
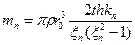 - приведенный момент инерции
- приведенный момент инерции
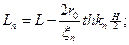
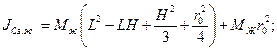
Проверки:
C совпадает с центром масс жидкости; свободной поверхности нет, тогда
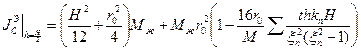 - по Жуковскому
- по Жуковскому
Полученное уравнение позволяет получать уравнение движения бака:
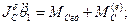
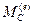 -момент внешних сил, действующих на бак.
-момент внешних сил, действующих на бак.
Если тело полностью заполнено жидкостью, то по Жуковскому (вокруг ц.м.):
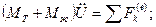
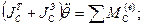
Теорема Жуковского «О движении твердого тела с полостями, полностью заполненными однородной несжимаемой, капельной жидкостью»
Твердое тело, имеющее полость, целиком заполненную однородной капельной жидкостью, движется как преобразованное твердое тело, масса которого равна сумме 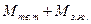 , а моменты инерции равны сумме
, а моменты инерции равны сумме 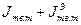 (эквивалентного тела).
(эквивалентного тела).
Для анализа гидродинамики используем модель – механическая модель.
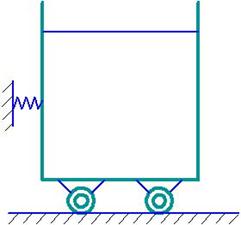
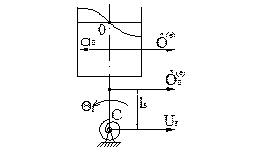
Рассмотрим (составим) уравнение поступательного движения бака с жидкостью с предположением механической модели.
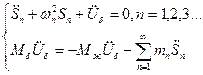
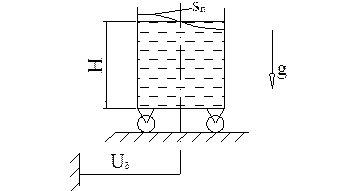 (I)
(I)
Механическая модель:
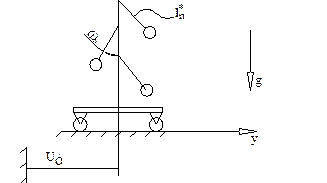 Дано:
Дано: 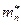 , масса телеги-
, масса телеги- 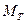 ,
, 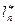
Число маятников 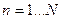
Составим уравнения движения системы:
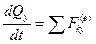 - уравнение количества движения,
- уравнение количества движения,
Где 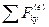 - все силы
- все силы
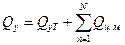 , причем
, причем 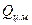 надо писать для абсолютных скоростей.
надо писать для абсолютных скоростей.
 Тогда
Тогда 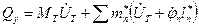 , где (1)
, где (1)
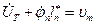 -абсолютная скорость
-абсолютная скорость
Уравнение для обобщенной координаты 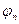 :
:
Ведем Даламберову силу:
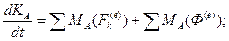
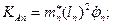
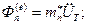
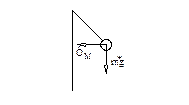 Из (1):
Из (1):
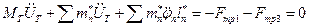 ,
,
Степеней свободы N+1
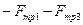 -не учитываем
-не учитываем
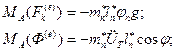
Тогда 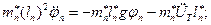
Т.к. колебания малые, то введем линейную координату (обобщенную координату отклонения маятника):
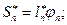
Тогда 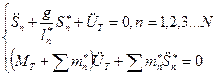 (II)
(II) 
Сравним с (I)
Если 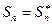 , число ступеней
, число ступеней 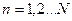
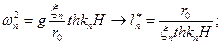
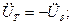
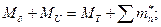
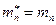
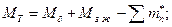
То (I) и (II) аналогичны.
Лекция №10 (10.10.06)
Механическая модель вращательного движения
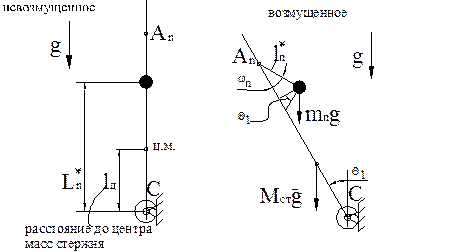
Дано: известен момент инерции стержня- 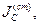
Масса стержня- 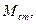
Число маятников- 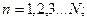
Центр масс стержня- 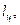
Масса маятника- 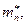
Решение:
Составим уравнение движения:
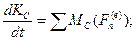 (1)
(1)
Где 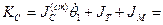
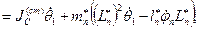 где
где 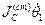 -кинетический момент стержня;
-кинетический момент стержня;
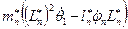 - кинетический момент маятника;
- кинетический момент маятника;
Или 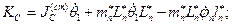
С другой стороны
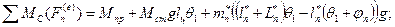
Тогда уравнение (1) примет вид:
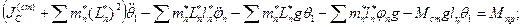
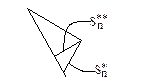 Примем
Примем 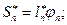
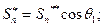
Или 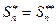 при малых колебаниях,
при малых колебаниях,
Тогда для стержня с маятником: 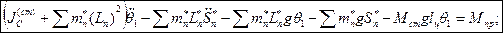 (2)
(2)
Тогда для бака:
(3)
Составим уравнения для маятников:
Теорема изменения кинетического момента в относительном движении:
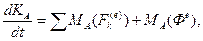 (4) где
(4) где
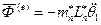 - сила инерции – Даламберова сила:
- сила инерции – Даламберова сила:
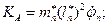
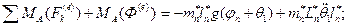
Тогда уравнение (4) примет вид:
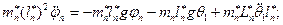
И окончательно:
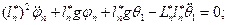 (5)
(5)
Пусть 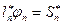 , тогда уравнение (5) будет:
, тогда уравнение (5) будет:
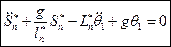 -для маятника
-для маятника 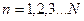 (6)
(6)
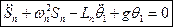 -для бака
-для бака 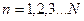 (7)
(7)
Сравнивая, получим из (2) и (3):
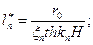
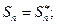
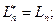
А из (6) и (7), получим:
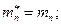
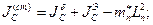
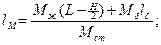
Уравнения плоского движения
Предположения:1) твердая крышка,
2) поправка к уравнению: постоянная сила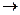 проекция от инерции вращения и наоборот
проекция от инерции вращения и наоборот
Дифференциальные уравнения плоского движения бака с жидкостью и стержня с маятником.
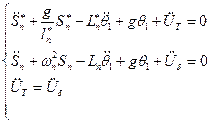 (6) и (7) неизменны, только добавляется ускорение от движения бака:
(6) и (7) неизменны, только добавляется ускорение от движения бака:
-для системы маятник-стержень
-для бака
Уравнение поступательного движения бака:
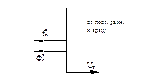
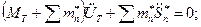
Уравнение поступательного движения стержня:
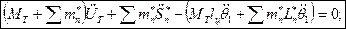
Уравнение плоского движения стержневой конструкции
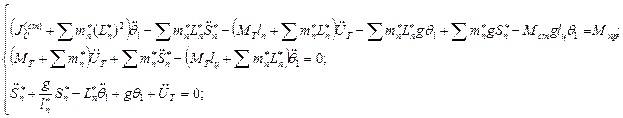 Для бака с жидкостью:
Для бака с жидкостью:
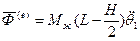
Уравнения для бака с жидкостью:
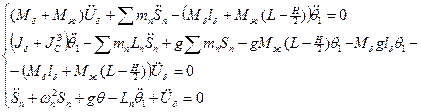
В дальнейшем предположим, что вращение вокруг центра масс системы:
1) бак + жидкость
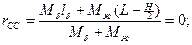
2) для маятникового аналога:
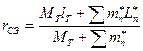 (система эквивалентна);
(система эквивалентна);
Тогда система уравнений упрощается и имеет вид:
для бака: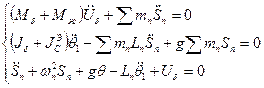
для стрежня: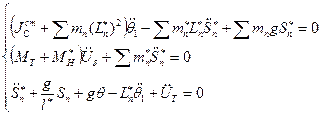
Отклонение свободной поверхности при вращательном движении
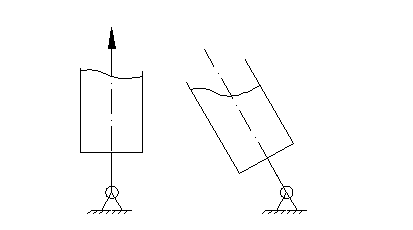
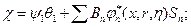
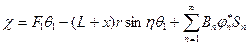
Окончательно получим:
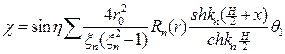
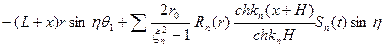 ;
;
Где 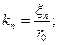
Обозначим: 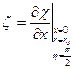 - смещение свободной поверхности.
- смещение свободной поверхности.
Тогда 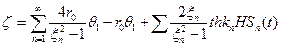 ,
,
т.к. 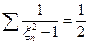 , то
, то
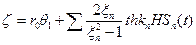 ,где
,где
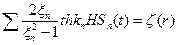
Пусть 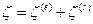 и
и 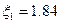
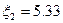
Тогда в связанной системе координат:
Если жидкость глубокая, то 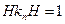
И тогда 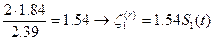
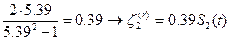
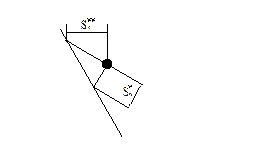
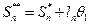
Лекция №11 (13.11.2006)
Уравнения колебаний свободной поверхности жидкости в обобщенных координатах для случая произвольно перемещающегося подвижного сосуда.
Тело совершает малые движения.
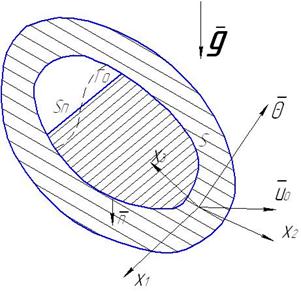
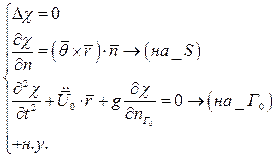
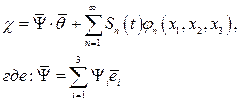
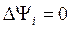
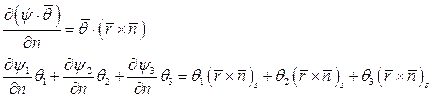
Тогда граничное условие для потенциала 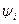 :
:
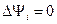
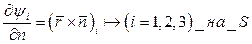
Подставим уравнение для 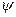 в уравнение для свободной поверхности.
в уравнение для свободной поверхности.
Считается, что 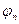 - решения для неподвижного сосуда – известны.
- решения для неподвижного сосуда – известны.
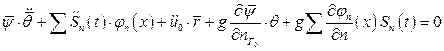
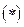 на Г0
на Г0
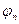 определяется из решения краевой задачи:
определяется из решения краевой задачи:
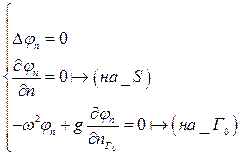
В «безразмерном» виде:
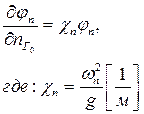
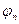 и их производные по нормали образуют базис
и их производные по нормали образуют базис 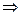
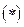 домножим на
домножим на 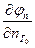 :
:
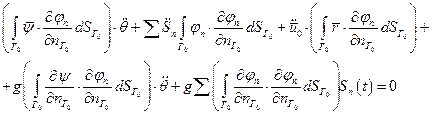
Формула Грина:
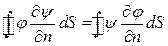
Для замыкания поверхности мысленно прибавляем поверхность, заполненную жидкостью, но 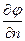 на дополнительной поверхности =0.
на дополнительной поверхности =0.
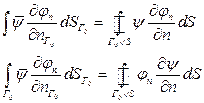
Берем условия для жесткой крышки:
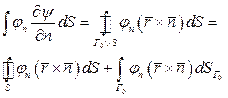
Для того, чтобы коэффициент уравнения для координации 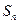 имели физический смысл домножим условия на свободной поверхности на плотность жидкости.
имели физический смысл домножим условия на свободной поверхности на плотность жидкости.
Введем обозначения:
 2014-02-10
2014-02-10 1261
1261






