Закон больших чисел.
Теорема. Пусть 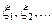 – последовательность независимых одинаково распределенных случайных величин (i.i.d.r.v.) с
– последовательность независимых одинаково распределенных случайных величин (i.i.d.r.v.) с 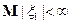 ,
, 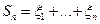 , и
, и 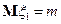 . Тогда
. Тогда
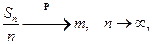
т.е. 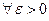
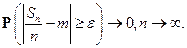
Доказательство. Пусть
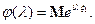
Тогда 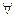 фиксированного
фиксированного 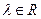
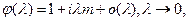
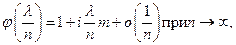
и
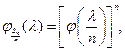
следовательно,
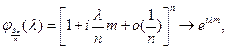
таким образом,
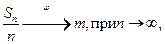
и, следовательно,
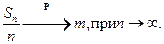
Теорема доказана.
Теорема. Пусть 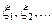 – последовательность независимых одинаково распределенных случайных величин (i.i.d.r.v.), невырожденных с
– последовательность независимых одинаково распределенных случайных величин (i.i.d.r.v.), невырожденных с 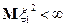 , и
, и 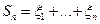 . Тогда при
. Тогда при 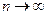
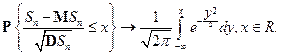
Доказательство. Пусть 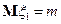 ,
, 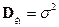 и
и 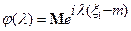 ,
,
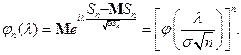
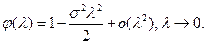
При фиксированном 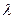 и
и 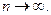
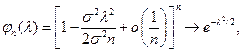
но 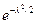 – характеристическая функция
– характеристическая функция 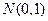 , так как
, так как
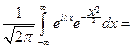
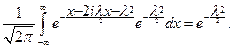
Теорема доказана.
Для вектора 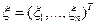 характеристическая функция
характеристическая функция
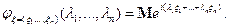
Теорема. Компоненты вектора 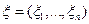 независимы тогда и только тогда, когда характеристическая функция вектора равна произведению характеристических функций его компонент.
независимы тогда и только тогда, когда характеристическая функция вектора равна произведению характеристических функций его компонент.
Доказательство. Необходимость очевидна.
Докажем достаточность.
Пусть 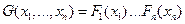 .
.
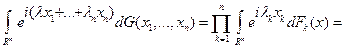
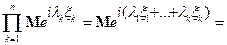
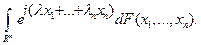
Следовательно, 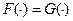 . Теорема доказана.
. Теорема доказана.
Для гауссовского вектора с плотностью
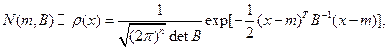
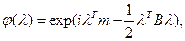
и некоррелированность компонент эквивалентна их независимости.
6. Условные математические ожидания
Условная вероятность относительно конечного разбиения 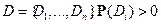
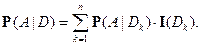
Условная вероятность простой случайной величины 
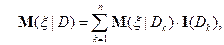
где
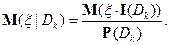
Данная формула, очевидно, обобщается на случай произвольной интегрируемой случайной величины.
Предложение. Для случайной величины с 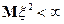
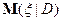 – оптимальная в среднеквадратическом смысле проекция
– оптимальная в среднеквадратическом смысле проекция  на
на 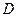 т.е., если
т.е., если 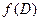 – оценка
– оценка  , то
, то
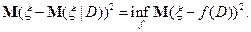
Доказательство. Для произвольной функции 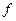
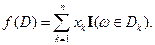
Тогда
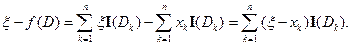
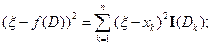
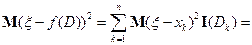
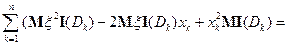
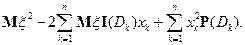
Так как это точка экстремума, то
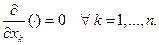
Следовательно,
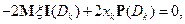
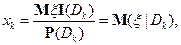
следовательно,
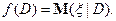
Построим для 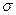 -алгебры
-алгебры 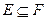 (пример
(пример 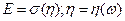 )
) 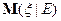 .
.
Обобщая
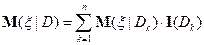
с
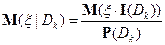
на случай 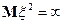 (когда нельзя говорить об
(когда нельзя говорить об 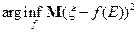 ) введем
) введем
Определение. Условным математическим ожиданием случайной величины  относительно
относительно 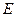 называется случайная величина
называется случайная величина 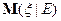 такая, что
такая, что
1) 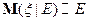 (т.е.
(т.е. 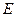 -измерима)
-измерима)
2) 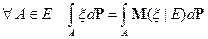 .
.
 2014-02-12
2014-02-12 356
356







