Доказательство 2)

Воспользумся вспомогательным утверждением.

Утверждение. a) Если любая слабо сходящаяся подпоследовательность 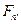сходится к одной и той же 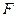, то и вся последовательность , .

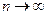б) Если 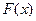– функция распределения и 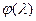её характеристическая функция, то существует константа 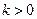такая, что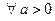

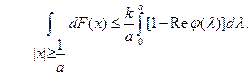
Доказательство утверждения.

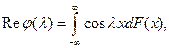
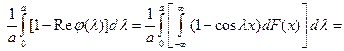
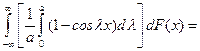
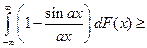
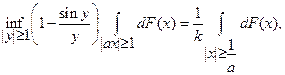
где

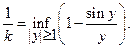
Утверждение доказано.

Доказательство 2). Пусть 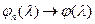, , 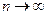где 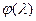непрерывна в 0. Покажем, что меры 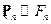плотны, т.е.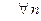

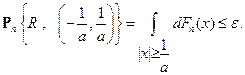
Действительно,

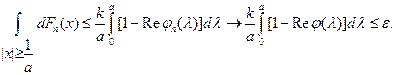
Так как 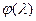непрерывна в нуле, то мы можем выбрать 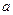и получить, что семейство плотно.

По теореме Прохорова из плотности следует относительная компактность, т.е. в каждой последовательности выбранной из 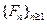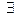слабо сходящаяся подпоследовательность 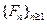, и, следовательно, в силу пункта a) утверждения следует требуемая сходимость. Теорема доказана.