Конечный автомат называется автоматом Мура, если его функция выходов зависит только от его состояний. Общая модель конечного автомата, рассмотренная ранее, называется автомат Милли.
Несмотря на то, что автомат Мура – частный случай более общего автомата Милли, алгоритмические возможности этих автоматов совпадают. Возможно автомат Мура заменить автоматом Милли.
Способы задания конечных автоматов
Конечный автомат можно задавать различными способами. Рассмотрим наиболее распространённые:
– табличный способ - функции δ, λ задаются таблицами;
– графический - конечный автомат задаётся специальной диаграммой на которой внутренние состояние автомата задаётся вершинами графа, а функции переходов и выходов - дугами, помеченными входными и выходными сигналами
– в виде блок-схемы.
В качестве примера рассмотрим конечный автомат, который для любой пары двоичных чисел вычисляет сумму. При этом работа автомата начинается с младших разрядов двоичного числа и числа обрабатываются справа налево.
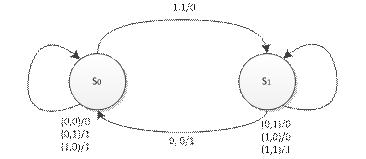
Таблица ХхS->S
| X S | S0 | S1 |
| S0 | S0 | |
| S0 | S1 | |
| S0 | S1 | |
| S1 | S1 |
| X S | S0 | S1 |
Блок-Схема

Протоколы и интерфейсы. Классическим для КА является введение понятия «внешние события», наступление, которых можно считать условиями перехода автомата в новое состояние. Такими событиями можно считать прерывание или срабатывание таймера. С ним естественно связывается понятие времени в автоматах. Действительно, введенные понятия времени в А можносвязать с ограничением пребывания А в некоторомконкретном состоянии. Такое ограничение задать таймером. Срабатывание таймера означает переход автомата в новое состояние.
КА бывают синхронными и асинхронными.
Синхронные КА управляются синхроимпульсами, которые поступают через равные промежутки времени.
Асинхронные КА управляются внешними событиями, наступление которых не всегда четко регламентировано. Такое управление иногда называют событийным, т.к. переход в новое состояние определяется событием, наступление которого не подлежит строгой регламентации.
В качестве примера рассмотрим спецификацию процесса, определяющего одинарный или двойной щелчок кнопки мыши (Double Click = 250 мс):
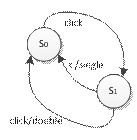
По клику автомат переходит в состояние S1, если до истечения 250мс. не поступает второго клика, то single, иначе double
Теория комплектов – дальнейшее развитие теории множеств. Комплект (К), как и множество, является набором некоторых элементов из определенного собрания элементов.
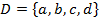

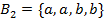
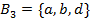

В отличие от множеств, комплекты допускают наличие нескольких экземпляров одного и того же элемента. Как известно, в любое множество элемент может либо входить, либо нет, а в комплект любой элемент может входить произвольное число раз. В представленных комплектов, К B1 и B3 являются множествами, т.к. каждый элемент входит в данный К только один раз. К-ы В2 и В4 равны, т.к. порядок вхождения отдельных элементов в К не важен. Это свойство К аналогично множетсву.
Для записи К используется функция числа экземпляров элементов, входящих в комплект: #(x,B). Это означает количество вхождений элемента x в В. Если ограничить число вхождений элемента x в В следующим соотношением: 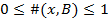 , то К превращается в множество.
, то К превращается в множество.
Подобно теории множеств, элемент x входит в комплект В только в том случае, если выполняется соотношение #(x,B)>0
Основатель теории множеств – Георг Кантор: «Множество – многое, мыслимое как единое».
После создания теории множеств, эта теория легла в основу многих математических моделей, и в настоящее время является фундаментом математики. Подобно теории Мн-в, в теории К допускается комплект, который не содержит ни одного элемента. Этот комплект называется пустым и обозначается #(x,B)=0.
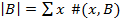 – мощность комплекта – общее число экземпляров в данном комплекте.
– мощность комплекта – общее число экземпляров в данном комплекте.
Если в теории множеств существует понятие подмножество, то в теории комплектов – подкомплект. Комплект А является подкомплектом 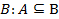 , если число вхождений каждого элемента в комплект А по крайней мере не больше числа вхождений этого элемента в комплект В, т.е.:
, если число вхождений каждого элемента в комплект А по крайней мере не больше числа вхождений этого элемента в комплект В, т.е.: 
 – равные комплекты
– равные комплекты
Подобно теории множеств, нулевой комплект может входить в любой комплект.
В теории комплектов определены четыре операции:
1) Объединение: 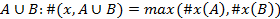
2) Пересечение: 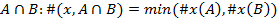
3) Сумма: 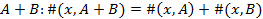
4) Разность: 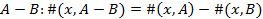
Можно показать, что объединение, пересечение и сумма коммутативны и ассоциативны. Подобно этому, такие соотношения имеются в теории множеств.
Разность комплектов ограничена условием: #(x,A)>#(x,B), т.к. число вхождений любого элемента в любой комплект не может быть отрицательным.
Для К справедливы соотношения:
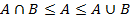

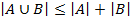

Назовем множество элементов, из которых образуются комплекты, областью D. Пространство комплектов Dn – множество всех таких К, элементы которых принадлежат области D и ни один элемент не входит в комплект более n раз.
Множество D∞ – множество всех К над областью D без какого либо ограничения на число вхождений экземпляров любого элемента в комплект.
Сеть Петри, как математический объект, состоит из четырех компонентов, которые определяют её структуру: C=(P,T,I,O), где:
P – position – множество позиций сети П;
T – transition – множество переходов;
I – in – входная функция;
O – out – выходная функция.
I и O связаны с переходами и позициями.
Входная функция I отображает переход Tj в множество позиций I(tj) – входные позиции перехода.
Выходная функция O отображает переход Tj в множество позиций O(tj) – выходные позиции перехода.
Таким образом, функция 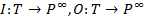 т.е. количество позиций во входной и выходной функциях не ограничено.
т.е. количество позиций во входной и выходной функциях не ограничено.
Сеть Петри является математический структурой C=(P,T,I,O), где:
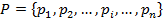

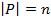 – мощность множества позиций
– мощность множества позиций
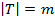 – мощность множества переходов
– мощность множества переходов
Произвольный элемент множества позиций обозначается 
Произвольный элемент множества переходов обозначается 
Позиция 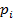 является входной позицией перехода
является входной позицией перехода 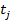 , если
, если 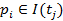
Позиция 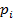 является выходной позицией перехода
является выходной позицией перехода 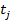 , если
, если 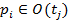
Выходы и входы переходов представляют собой комплекты позиций. Кратность входной позиции для 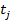 – число появлений позиции
– число появлений позиции 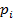 во входном комплекте перехода, что математически изображается:
во входном комплекте перехода, что математически изображается: 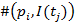 . Аналогично, кратность выходной позиции
. Аналогично, кратность выходной позиции 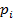 для перехода
для перехода 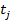 – число появлений позиции
– число появлений позиции 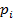 в выходном комплекте переходов:
в выходном комплекте переходов: 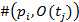
Определим расширенную входную функцию I и выходную функцию O таким образом, что:
 =
= 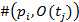
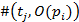 =
= 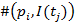
 2014-02-12
2014-02-12 740
740








