Основы теории конечных автоматов

Все автоматы делятся на:

А) Комбинационные (без памяти)

Б) Конечные (с памятью/последовательные устройства)

А) Называются функциональными преобразователями т.к. они преобразуют вектор входных сигналов в вектор выходных сигналов на основе использования логическихэлементов. Эти автоматы имеют единственное внутреннее состояние, которое определяется логическими функциями, которые участвуют в переработке информации, т.к. у них единственное внутреннее состояние, тоэти автоматы называются автоматами без памяти.

Б) Являются более сложными устройствами чем А). Их реакция зависит не только от вектора входных сигналов в данный момент, но и от того какие сигналы, но и от того какие сигналы поступили на вход ранее, т.е. от входной истории. На один и тот же входной сигнал конечный автомат реагирует по-разному, в зависимости от того в каком состояние он находился ранее, т.е. выходной сигнал конечного автомата зависит от входной истории.

Т.к. число входных историй конечного автомата счётно, но бесконечно, то для того, чтобы реагировать по-разному на все бесконечные входные истории, он должен был бы иметь бесконечную память. Чтобы избежать этого, входные автоматы делят на классы эквивалентных состояний; в эквивалентный класс входят все те состояния, на которые автомат реагирует одинаковым образом. Число таких эквивалентных состояний конечно, не смотря на то что общее число вероятных состояний А бесконечно, но счётно. Такая упрощённая модель с конечным числом внутренних эквивалентных состояний получила название конечный автомат. Т.к. число эквивалентных внутренних состояний конечно, то для реализации такой математической модели достаточно иметь конечное число элементов памяти.

С математической точки зрения конечным автоматом (Автомат Мили) называется математический объект, обладающий свойствами:

A=<S,X,У,S₀,δ,λ> где

S- конечное множество внутренних состояний А.

Х- конечное число входных сигналов А (входной алфавит)

У – конечное число выходных символов А (выходной алфавит)

S₀єS- начальное/инициальное состояние А

^* δ – Функция перехода δ:S×X->S^*

^** λ это λ:S×X->y функция выходов

^* отображение декартова множества внутренних состояний на множество входных сигналов.

^** отображение декартова множества внутренних состояний на множество выходных сигналов.

2 конечных автомата считаются эквивалентными, если их отображения «вход-выход» эквивалентны. Напоминаем, что 2 логические функции F1 и F2 эквиваленты если на всех наборах аргументов их значения одинаковы, но, как известно, количество наборов переменных для каждой функции ограниченно => достаточно сравнить полученные значения функций F1 и F2 на всех наборах переменных.

Иное дело с конечными А. Как известно, количество внутренних состояний А бесконечно (но счётно)=> говорить об эквивалентности конечных автоматов достаточно сложно; задача определения эквивалентности конечных автоматов не является тривиальной.

Пусть A=<S,X,y,S₀,δ,λ>- конечный автомат. Рассмотрим функции перехода S и выхода λ так, чтобы они были определены на множествах последовательностей (цепочках) сигналов входного алфавита. Если Х- алфавит входного сигнала, то через Х* обозначим множество последовательностей входных сигналов. Обозначим малыми греческими буквами α,β,γ последовательности в такихсигналах, e(empty) тогда αE=Eα=α

Расширенными функциями переходов и выходов автомата называют:

δ^*:X^*×S->S

λ^*:X^*×S->y

δ^*(S, α,a_j)=δ(δ^*(S,α)a_j)

λ^*(S, α,a_j)= λ^*(δ^*(S,α)a_j) α=a_j1,a_j2…a_jk

δ^*(S_i,a_j1,a_j2..a_jk)= δ(δ(..δ(S_ia_j1)a_j2..)a_jk)

λ*(S_i, α,a_j)= λ(S^*(S_iα)a_j)

w= λ(Siaj1)^ λ((Siaj1)aj2)^ λ ((Siaj1)aj2)aj3

Для данного автомата и его функций δ, λ расширенные функции δ*, λ* определены на множестве входных сигналов. Индуктивноеопределение расширенных функций δ*, λ* представляет формулу в компактном виде. Для более детального понимания существа процесса предполагается традиционное определениерасширенных функций δ*, λ* с многоточиями и скобками. Это определение намного точнее и лучше определяет смены расширенных функций δ*, λ*.

Если результатом применения автоматного оператора к входному слову α является выходное слово w то это можно записать A(S₀, α)=w это означает,что А, находясь в некотором начальном состояние S₀ при поступление на его вход некоторой цепочки входных сигналов α выдаёт последовательность выходных сигналов w.

Более кратко: A(α)=w

Причём длина входного слова α равна длине выходного слова w: | α |=|w| l(α)=l(w)

Пусть A=<S,X,y,S₀,δ,λ> - конечный автомат

S_iєS – называется достижимым тогда, когда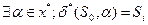

Состояние S_iєS называется достижимым тогда и только тогда, когда под воздействием какой-либо цепочки входных сигналов автомат попадает в это состояние из состояния S₀.

Состояние Si является недостижимым тогда и только тогда, когда под воздействием любой цепочки входных сигналов автомат не попадает в это состояние из состояния S₀.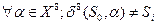

А называется сильносвязным если из любого его состояния достижимо другое его состояние.

А называется частичным / не полностью определённым если одна из двух функций (δ, λ) не полностью определена. В таком А для некоторых состояний не определены значения δ,λ; В автоматной таблице неполная определенность автомата выражается в том, что некоторые клетки её не заполнены.