Пусть имеется полная группа несовместных событий 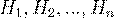 (гипотез), вероятности которых известны.
(гипотез), вероятности которых известны.
Производится испытание, в результате которого осуществляется событие  . Условные вероятности данного
. Условные вероятности данного
события по отношению к каждой гипотезе тоже известны. В этом случае можно пересчитать вероятности гипотез
в связи появлением события  , вычислить их можно по формуле:
, вычислить их можно по формуле:
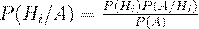 (22)
(22)
которая называется формулой Бейеса (или Байеса).
Пример 29. На складе находятся детали, изготовленные на двух заводах. Известно, что объем продукции
первого завода в 4 раза превышает объем продукции второго завода. Вероятность брака на первом заводе 0,05;
на втором- 0,01. Наудачу взятая деталь оказалась бракованной. Найти вероятность того, что она изготовлена на
первом заводе.
Решение. Обозначим событие  ={деталь бракованная},
={деталь бракованная}, 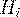 ={деталь изготовлена на i-ом заводе}, где i=1,2.
={деталь изготовлена на i-ом заводе}, где i=1,2.
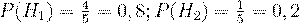 . По условию
. По условию 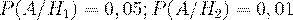 ,
,
тогда по формуле (22) находим 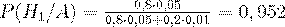 .
.
Вопрос. Чему равна сумма вероятностей гипотез?
заранее не известно
0,5
 2014-02-12
2014-02-12 2523
2523







