2014-02-12
403Таблица 3.5
Таблица 3.4
Расчет дисперсии результатов тестирования 15 учеников 3-го класса
| № пп | xi | xi 2 | № пп | xi | xi 2 | |
| 44 944 | 55 225 | |||||
| 49 729 | 50 625 | |||||
| 50 625 | 51 984 | |||||
| 43 264 | 63 504 | |||||
| 52 900 | 56 169 | |||||
| 46 656 | 60 516 | |||||
| 58 081 | 47 961 | |||||
| 40 804 | ||||||
| Сумма | 3 399 | 772 987 |
Пример 3.13. Найдите дисперсию и стандартное отклонение результатов тестирования для сгруппированных данных (ТЕСТ №1) по данным таблицы 3.2.
Решение. По формуле (3.6) имеем Dx =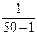
(1 193 856 – 
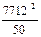)» 88,92 (балла2). Тогда стандартное отклонение s = 
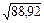» 9,43 (балла). Промежуточные расчеты приведены в таблице 3.5.
Ответ: 9,43.
Чем сильнее значения вариационного ряда отклоняются от своего среднего значения, тем больше величина дисперсии и стандартного отклонения.
Расчет дисперсии результатов тестирования (ТЕСТ №1)
| № пп | xi * (баллы) | ni | nixi * | nixi *2 |
| 16 384 | ||||
| 36 992 | ||||
| 1 296 | 186 624 | |||
| 2 280 | 346 560 | |||
| 2 720 | 435 200 | |||
| 141 120 | ||||
| 1 76 | 30 976 | |||
| Сумма | 7 712 | 1 193 856 |
Пример 3.14. Рассмотрим два статистических ряда (рис. 3.9). Нетрудно видеть, что` x = 50,` y = 50. Однако, Dх = 
(302+402+602+702 - 4·502) = (11000 - 10000)» 333,33, Dy = (482+492+512+522 - 4·502) = (10010 - 10000)» 3,33, s х» 18,26, s у» 1,826. Это говорит о том, что данные первого статистического ряда менее разбросаны около своего среднего значения.
| xi | yi | |||||||||
| ni | ni |
Рис. 3.10
На рис. 3.11 приведены примеры распределений частот значений трех переменных с одинаковыми средними, но различными дисперсиями. С уменьшением s график делается уже и вытягивается вдоль прямой x =` x.
 |
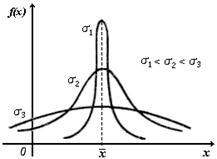Частотное распределение данных для трех переменных
с равными значениями средних, но различным разбросом
Рис. 3.11
Пример 3.15. В таблице на рис. 3.12 представлены сведения о дневной выработке двух рабочих, которые изготовляли одинаковые детали. Сравните стабильность работы рабочих.
Решение. Легко посчитать, что каждый рабочий за 5 дней изготовил 250 деталей, значит, средняя производительность труда за день у обоих рабочих одинаковая:` x =` y = 50 дет./день. Моды у предложенных совокупностей отсутствуют, а медианы тоже одинаковые (50 и 50). Поэтому в данном случае в качестве критерия сравнения совокупностей может выступать стабильность производительности труда рабочего. Ее можно оценивать с помощью дисперсии.
С помощью таблицы (см. рис. 3.13) найдем суммы квадратов отклонений от средних значений величин X и У. Тогда Dх =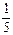 
· 40 = 8, Dy = 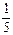· 282 = 56,4. Видим, что Dх < Dy, значит, первый рабочий работает стабильнее второго. На практике это означает, что второй рабочий имеет нестабильную производительность труда: в какие-то дни работает не в полную силу, а в какие-то наверстывает упущенное, что всегда сказывается на качестве продукции.
Ответ: первый рабочий работает стабильнее второго.
| День недели | Дневная выработка (количество деталей) | |
| первого рабочего (X) | второго рабочего (У) | |
| Понедельник | ||
| Вторник | ||
| Среда | ||
| Четверг | ||
| Пятница |
Рис. 3.12
| День недели | Значение случайной величины | Отклонение от среднего ` x =` y = 50 | Квадраты отклонений | |||
| xi | yi |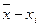 
| 
| 
| 
| |
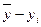
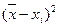
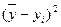
| Понедельник | 2 | |||||
| Вторник | -10 | |||||
| Среда | ||||||
| Четверг | -2 | |||||
| Пятница | -4 | -6 | ||||
| Сумма |
Рис. 3.13
1. Задачі вивчення дисципліни СтМЗРО та її коротка характеристика
