Пусть дано уравнение
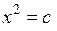 , (8.6)
, (8.6)
где с – действительное число. Требуется решить его в комплексных числах, т.е. найти все комплексные числа 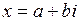 , которые удовлетворяют уравнению (8.6).
, которые удовлетворяют уравнению (8.6).
Допустим, что существует комплексное число 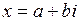 (
(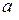 и
и 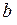 – действительные числа), удовлетворяющее уравнению (8.6). Подставим его в (8.6) и произведем соответствующие преобразования
– действительные числа), удовлетворяющее уравнению (8.6). Подставим его в (8.6) и произведем соответствующие преобразования
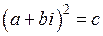 ,
, 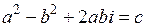 .
.
Так как с –действительное число, то
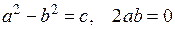 . (8.7)
. (8.7)
Из второго равенства следует, что по крайней мере одно из чисел 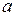 ,
, 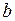 равно нулю.
равно нулю.
Пусть с = 0, тогда 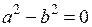 и
и 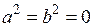 , т.е.
, т.е. 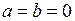 .
.
Пусть с > 0. Так как из второго уравнения (8.7) следует, что одно
из чисел 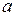 ,
, 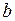 равно нулю, то из первого следует, что
равно нулю, то из первого следует, что 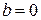 , и мы получим уравнение
, и мы получим уравнение 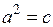 , где надо искать действительные числа
, где надо искать действительные числа 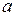 . Это уравнение имеет два решения (корня):
. Это уравнение имеет два решения (корня): 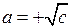 и
и 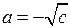 ,
,
где 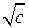 – арифметическое значение квадратного корня из с. Мы получили
– арифметическое значение квадратного корня из с. Мы получили 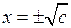 .
.
Если теперь с < 0, то значит 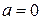 , а
, а  , и тогда
, и тогда 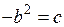 или
или 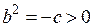 , откуда
, откуда 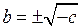 и, следовательно,
и, следовательно, 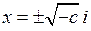 .
.
Таким образом, если с > 0, то уравнение (8.6) имеет два действительных решения 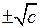 и комплексных решений не имеет;
и комплексных решений не имеет;
если с < 0, то уравнение (8.6) имеет два чисто мнимых решения 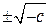 ; при с = 0 имеется только одно решение: х = 0.
; при с = 0 имеется только одно решение: х = 0.
|
|
|
Любое комплексное число х, удовлетворяющее уравнению (8.6), называют корнем квадратным из числа с и обозначают символом 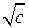 .
.
Рассмотрим квадратное уравнение в общем виде
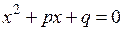 , (8.8)
, (8.8)
где 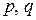 –заданные действительные числа.
–заданные действительные числа.
Будем искать комплексные решения этого уравнения. Пусть комплексное число  является решением уравнения (8.8). Тогда
является решением уравнения (8.8). Тогда
 ,
, 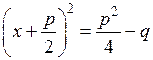 .
.
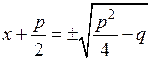 ,
,
где слева стоит любое комплексное число, квадрат которого
равен 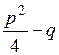 .
.
Отсюда получаем формулы для нахождения решений квадратного уравнения
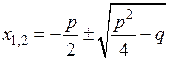 при
при 
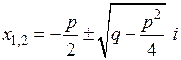 при
при 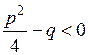 .
.
Итак, квадратное уравнение (8.8) в случае, когда 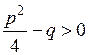 , имеет два действительных решения, а в случае, когда
, имеет два действительных решения, а в случае, когда 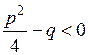 , – два комплексно-сопряженных решения. В случае же
, – два комплексно-сопряженных решения. В случае же 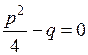 оно имеет одно решение, равное
оно имеет одно решение, равное 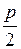 ; считают, что и в этом случае решений два, но они совпадают, и называют решение (корень) уравнения (8.8) кратным.
; считают, что и в этом случае решений два, но они совпадают, и называют решение (корень) уравнения (8.8) кратным.
Пример. Решить уравнение 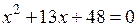 .
.
○ 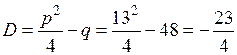 .
.
Так как 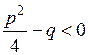 , то уравнение имеет два комплексно-сопряженных решения:
, то уравнение имеет два комплексно-сопряженных решения: 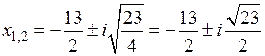 . ●
. ●
 2014-02-12
2014-02-12 381
381






