Производная сложной функции
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.
Тогда 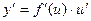
Рассмотрим функцию 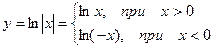 .
.
Тогда (lnïxï)¢= 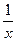 , т.к.
, т.к. 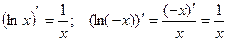 .
.
Учитывая полученный результат, можно записать 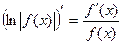 .
.
Отношение 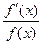 называется логарифмической производной функции f(x).
называется логарифмической производной функции f(x).
Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
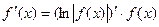
 2014-02-12
2014-02-12 339
339







