Прямая
Плоскость
 Общее уравнение плоскости a*Px+b*Py+c*Pz+d=0 или
Общее уравнение плоскости a*Px+b*Py+c*Pz+d=0 или 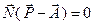 или
или 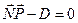 . Параметрически задается в виде
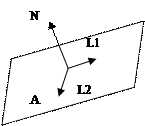
. Параметрически задается в виде 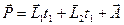 , где L1,L2 – два непараллельных вектора в плоскости.
, где L1,L2 – два непараллельных вектора в плоскости.
Расстояния от точки до плоскости 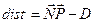 .
.
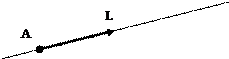 Уравнение прямой, проходящей, через две точки.
Уравнение прямой, проходящей, через две точки. 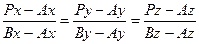
Является также пересечением двух плоскостей, и может быть задана в виде системы из двух уравнений плоскости 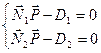 , либо параметрически
, либо параметрически 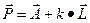 .
.
Получить направление и точку для параметрического задания можно следующим образом 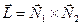 (должен лежать в обеих плоскостях, а значит – быть перпендикулярным обеим нормалям). А точку получить из пересечения трех плоскостей, двух исходных и третьей – с нормалью L и проходящей через начало координат. Получаем систему
(должен лежать в обеих плоскостях, а значит – быть перпендикулярным обеим нормалям). А точку получить из пересечения трех плоскостей, двух исходных и третьей – с нормалью L и проходящей через начало координат. Получаем систему
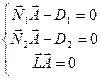 , ее решением будет
, ее решением будет  .
.
В конце имеет смысл нормализовать вектор L.
Расстояния от точки до прямой 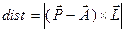 .
.
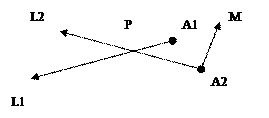
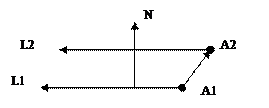 Расстояние между прямыми считается следующим образом, сначала находится направление, перпендикулярное обеим прямым
Расстояние между прямыми считается следующим образом, сначала находится направление, перпендикулярное обеим прямым 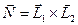 , а затем уже само расстояние, как проекция вектора A1A2 на это направление
, а затем уже само расстояние, как проекция вектора A1A2 на это направление 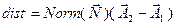 . Если же прямые параллельны (
. Если же прямые параллельны (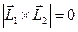 ), то расстояние считается как расстояние от точки одной прямой до другой, например,
), то расстояние считается как расстояние от точки одной прямой до другой, например, 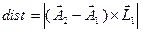 . Если расстояние равно нулю – прямые пересекаются (при параллельных прямых – коллинеарны).
. Если расстояние равно нулю – прямые пересекаются (при параллельных прямых – коллинеарны).
Две наиболее близкие точки прямых, проецируются в ту же точку, что и точка пересечения проекций прямых на плоскость с нормалью N. Поэтому можно воспользоваться формулами пересечения прямых для плоского случая. При этом плоскость задана базисом (L2,M) M=L2xN.
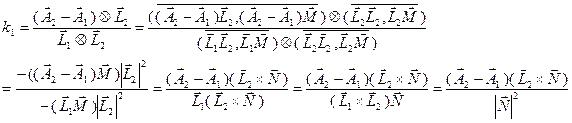
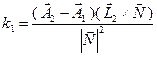 ,
, 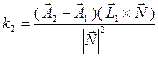
Пересечение прямой 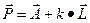 с плоскостью
с плоскостью 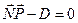 .
. 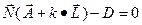 ,
, 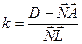 .
.
Сфера
Общее уравнение 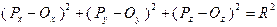 , или
, или 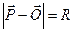
Практически все формулы остаются как у окружности.
Это тот же полигон, только плоскость, в которой он лежит имеет некоторую ориентацию в пространстве. Т.о. сохраняются все свойства и алгоритмы для полигона на плоскости. Нормаль к плоскости в которой лежит треугольник ABC 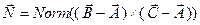 . Нормаль к плоскости в которой лежит произвольный полигон можно получить, либо взяв три неколлинеарные вершины, либо по формуле Ньэла.
. Нормаль к плоскости в которой лежит произвольный полигон можно получить, либо взяв три неколлинеарные вершины, либо по формуле Ньэла.
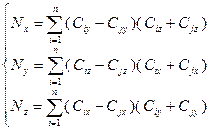 ,
, 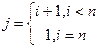
Конечно затем нужно нормализовать N.
Более простая формула Ньэла 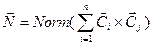 .
.
Все алгоритмы для 2D случая можно применять и в 3D, это можно делать тремя способами:
1. Совместить плоскость полигона с плоскостью OXY и далее работать как в 2D случае.
2. Работать с проекциями полигона (правда, в проекциях нельзя правильно посчитать площадь) на одну из ортогональных плоскостей OXY, OXZ, OYZ. Плоскость выбирается в зависимости от нормали (например, если максимальным является модуль компоненты z выбирается плоскость OXY).
3. Работать в 3D пространстве с некоторыми модификациями формул. В основном это касается pdp, оно заменяется на смешанное произведение 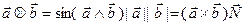 .
.
 2014-02-12
2014-02-12 664
664








