2014-02-12
761
ГЕОМЕТРИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРНОЙ ГРАФИКИ
В настоящее время существует большое число прекрасных курсов высшей математики, которая и является тем фундаментом, на котором построены все методы и алгоритмы компьютерной графики.
Тем не менее, авторы считают необходимым привести в качестве справочного материала некоторые сведения из курса аналитической геометрии и математического анализа, которые имеют отношение к тематике учебного пособия.
Рассмотрим различные способы представления векторов на плоскости и в пространстве. Пусть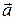 
некоторый вектор, заданный в декартовой системе координат 
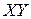на плоскости (рис.7.1) и декартовой системе координат 
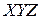в пространстве (рис. 7.2).
В прямоугольной системе координат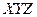 
направление осей задается тройкой перпендикулярных единичных векторов 
, 
, 
.
Система координат называется правой, если при повороте от вектора 
к вектору 
на 
направление вектора 
совпадает с поступательным движением винта с правой резьбой (рис. 7.3). Начальная точка векторов обозначается буквой О. Ниже представлены различные формы записи векторов на плоскости и в пространстве.
| 
|
| Рис.7.1 | Рис. 7.2 |
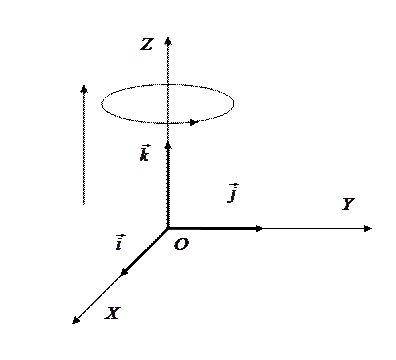
Рис. 7.3
(7.1)
(7.2)
Другая форма записи векторов
(7.3)
(7.4)
Модуль (длина) вектора
(7.5)
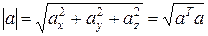(7.6)
Пусть заданы два вектора 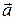и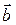 
в форме (7.4)
и 
,
Тогда
(7.7)
(7.8)
При этом справедливы равенства
(7.9)
