2014-02-12
1043
Скалярное произведение векторов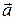 
и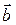 
определяется выражением
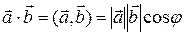, (7.10)
где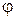 
- угол между векторам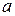и 
и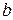 
В координатной форме
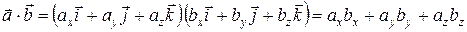(7.11)
Или
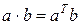, (7.12)
если вектора 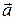и 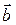представлены в форме (7.4).
Из (7.10) получаем
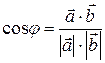(7.13)
Если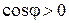 
, то угол между векторам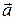и и 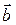является острым 
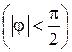, при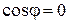 
– вектора 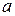и 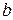ортогональны
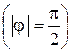, а если 
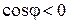, то угол между векторами является тупым 
.
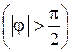Отметим некоторые свойства скалярного произведения.
Пусть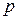 
,
,
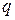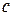- некоторые числа. Тогда справедливы равенства:
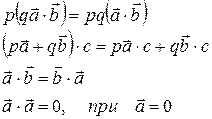(7.14)
