2014-02-12
1649
АФФИННЫЕ ПРЕОБРАЗОВАНИЯ НА ПЛОСКОСТИ
Пусть на плоскости задана система координат (СК)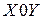 
и точка 
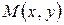принадлежащая некоторому объекту. Система координат 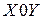трансформируется в СК 
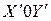путем ряда последовательных смещений и поворотов относительно своего исходного состояния. При этом точка 
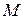(объект) остается неподвижной. Необходимо определить координаты точки 
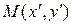(объекта) в системе координат 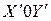(рис. 8.1а, рис 8.1б).
 |  |
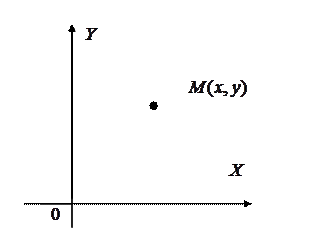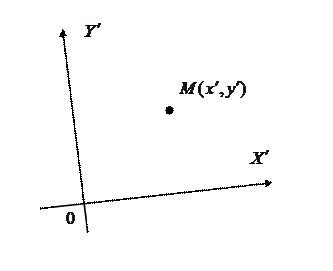| Рис. 8.1а | Рис. 8.1б |
В общем случае преобразование координат мочки 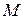при переходе от системы координат 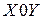к системе координат 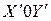определяется системой линейных уравнений:
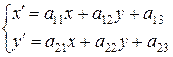, (8.1)
где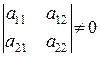 
Выражение (8.1) представляет собой аффинное преобразование координат при переходе от системы координат 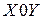к системе координат .
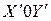Обратный переход от 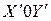СК к СК 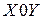определяется как
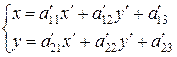, (8.2)
Афинное преобразование (8.1) удобно представить в матричном виде:
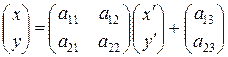(8.3)
В компьютерной графике принято использовать однородные координаты, которые вводятся следующим образом. Точке 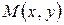ставится в соответствие точка 
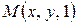, а точке 
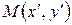точка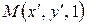 
.
Тогда переход от системы координат 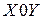к системе координат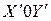в матричном виде можно записать как
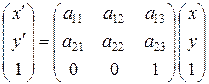(8.4)
или
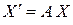, (8.5)
где
, 
,
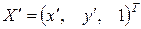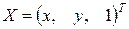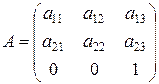(8.6)
Обратное преобразование
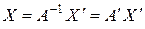, (8.7)
где
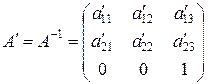(8.8)
Рассмотрим теперь различные виды афинных преобразований на плоскости и соответствующие им матрицы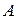 
и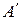 
.
Параллельный сдвиг системы координат (рис. 8.2)
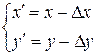, (8.9)
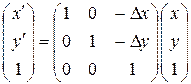(8.10)
Или
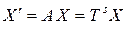, (8.11)
 |  |
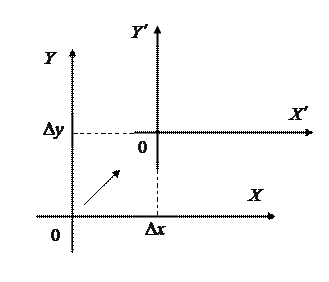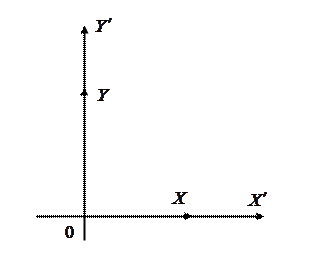| Рис. 8.2 | Рис. 8.3 |
где
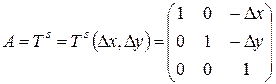(8.12)
Здесь и далее индекс «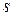
» означает, преобразованию подвергается система кординат.
