В данном разделе рассматривается задача вычисления вектора нормали к поверхности, которая возникает во многих задачах компьютерной графики.
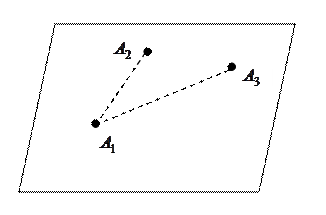
Сначала вычислим нормаль к плоскости, которая определяется расположенными на ней тремя точками (рис. 7.6).
 |  |
| Рис. 7.6 | Рис. 7.7 |
Пусть точки  ,
,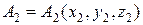 и
и 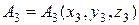 лежат в одной плоскости.
лежат в одной плоскости.
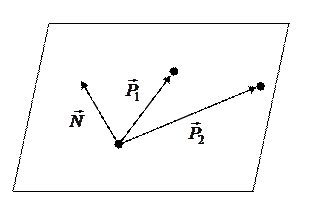
Образуем вектора
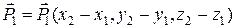 и
и 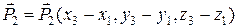 .
.
Тогда вектор нормали 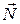 к плоскости можно вычислить как векторное произведение векторов
к плоскости можно вычислить как векторное произведение векторов 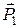 и
и 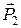
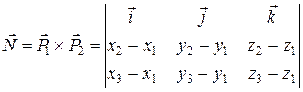 (7.44)
(7.44)
Выражение (44) используется для вычисления координат вектора нормали в случае описания поверхности векторно – полигональной моделью (см. ниже).
Рассмотрим теперь произвольную поверхность, заданную в явном виде функцией
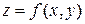 (7.45)
(7.45)
При таком задании поверхности вектор нормали будет имеет вид []
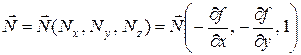 , (7.46)
, (7.46)
где 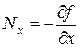 ,
,  ,
,  – координаты вектора нормали.
– координаты вектора нормали.
Единичный вектор нормали будет определяться выражением
 , (7.47)
, (7.47)
где 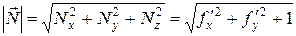 – модуль вектора нормали,
– модуль вектора нормали, 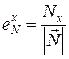 ,
, 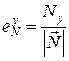 ,
, 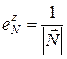 – координаты вектора единичной нормали.
– координаты вектора единичной нормали.
Пусть теперь поверхность задана неявно уравнением
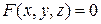 . (7.48)
. (7.48)
При неявном определении поверхности вектор нормали примет вид []
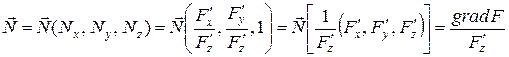 (7.49)
(7.49)
где 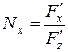 ,
, 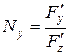 ,
,  – координаты вектора нормали,
– координаты вектора нормали,
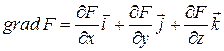 (7.50)
(7.50)
– градиент функции 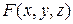 .
.
Единичный же вектор нормали в этом случае
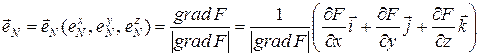 , (7.51)
, (7.51)
где
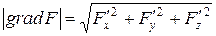 – (7.52)
– (7.52)
модуль градиента функции  ,
, 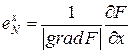 ,
, 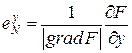 ,
, 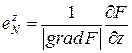 – координаты вектора единичной нормали.
– координаты вектора единичной нормали.
При выборе вектора нормали необходимо следить за тем, чтобы получить нормаль нужного направления, т. е. правильно выбрать нужную сторону поверхности []. Если для поверхности 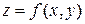 указано, что нормаль к ней составляет с осью
указано, что нормаль к ней составляет с осью 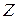 угол больший чем
угол больший чем  то вместо (46) в качестве вектора нормали необходимо взять вектор
то вместо (46) в качестве вектора нормали необходимо взять вектор
 , (7.53)
, (7.53)
Аналогично для поверхности 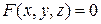 . В этом случае вместо (49) для вычисления вектора нормали следует воспользоваться выражением
. В этом случае вместо (49) для вычисления вектора нормали следует воспользоваться выражением
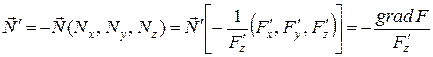 (7.54)
(7.54)
Соответственно выражение для вектора единичной нормали будет иметь вид
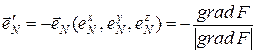 (7.55)
(7.55)
Рассмотрим пример (сфера)
Пусть теперь поверхность задана параметрически:
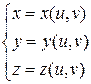 (7.56)
(7.56)
Тогда вектор нормали 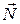 к поверхности имеет вид []:
к поверхности имеет вид []:
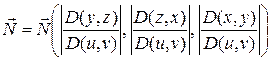 , (7.57)
, (7.57)
где
 ,
, 
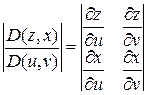 ,
, 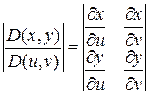 (7.58)
(7.58)
Рассмотрим пример (сфера)
 2014-02-12
2014-02-12 16612
16612