2014-02-12
369
При визуализации данных, полученных экспериментальным или расчетным путем, часто встречается задача построения линий уровня на поверхностях.
Пусть функция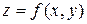 
определяет некоторую поверхность в декартовой системе координат 
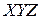. Тогда, геометрическое место точек 
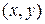, удовлетворяющее условию 
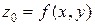, где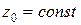 
, называется линией уровня. Линия уровня представляет собой результат сечения поверхности 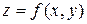плоскостью .
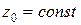Рассмотрим пример. Пусть поверхность определяется уравнением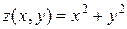 
(рис. 11.5).
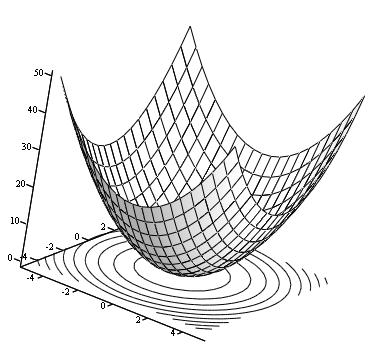
Рис. 5
Зададимся множеством плоскостей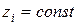 
, 
, 
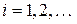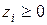. Теперь можно записать уравнение для линий уровня
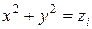(11.14)
Как видно из (14), линии уровня для рассматриваемой поверхности представляют собой окружности радиуса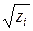 
с центром в начале координат (рис. 11.5).
В частности, линии уровня знакомы нам по географическим картам, на которых они служат для обозначения высоты местности над уровнем моря.
Рассмотрим общий подход к построению линий уровня.
Пусть поверхность 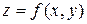задана массивом своих значений 
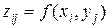, рассчитанных на сетке 
, 
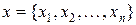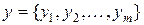(рис. 11.6).
|
|
|
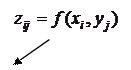
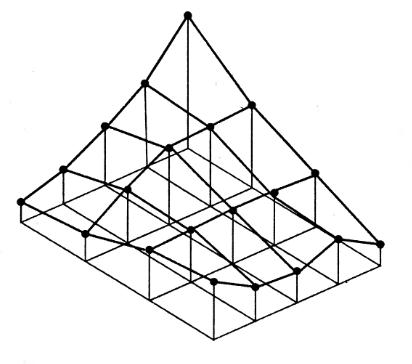
Рис. 11.6
Тогда процедура построения линий уровня заключается в следующем.
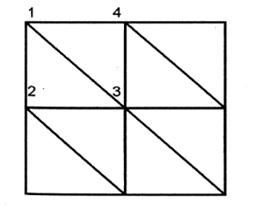
1. Выполняется триангуляция поверхности, каждая ячейка сетки разбивается на два треугольника (рис. 11.7).
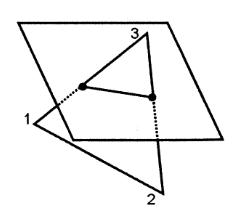
2. Для каждого треугольника находится пересечение с плоскостью 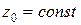(рис. 11.8).
|  
|
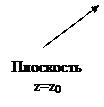
| Рис.7 | Рис.8 |
Этот метод достаточно прост и позволяет получить хорошее изображение линии уровня. Надо отметить, что линия уровня может быть с разрывами.
