Пусть в некоторой области пространства, в которой введены криволинейные координаты q 1, q 2, q 3, задано дифференцируемое векторное поле a (M). Найдем выражение дивергенции в ортогональных криволинейных координатах. По определению div a в точке M задается формулой:
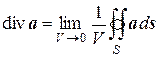 .
.
Следовательно, мы можем вычислить div a в точке M как отношение потока вектора a через поверхность бесконечно малого параллелепипеда, изображенного на рис. 9.1, к объему dv этого параллелепипеда. Обозначим a 1, a 2, a 3 компоненты вектора a в базисе e 1, e 2, e 3 и вычислим сначала поток этого вектора через две грани, перпендикулярные ребру MM 1.
Внешняя нормаль к грани MM 2 N 1 M 3 совпадает с вектором (– e 1). Следовательно, поток вектора a через эту грань (с точностью до бесконечно малых величин 1-го порядка относительно dv) равна
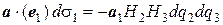 . (9.11)
. (9.11)
Противоположная грань M 1 N 3 NN 2 отличается от рассмотренной грани тем, что на ней первая криволинейная координата равна q 1+ dq 1; следовательно, значение величины a 1 H 2 H 3 на этой грани отличается от ее значения на грани MM 2 N 1 M 2 приращением:
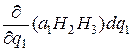 .
.
Кроме того, направление нормали к грани M 1 N 3 NN 2 совпадает с направлением вектора e 1. Поэтому поток вектора a через грань M 1 N 3 NN 2 равен
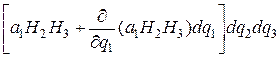 . (9.12)
. (9.12)
Сложив выражения (9.11) и (9.12), получим, что поток вектора a через две параллельные между собой грани MM 2 N 1 M 3 и M 1 N 3 NN 2 равен
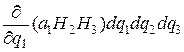 .
.
Аналогично рассматривая две другие пары параллельных между собой граней, получим следующие два выражения для потока векторного поля через эти пары граней:
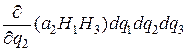 и
и  .
.
Складывая все три полученные величины и разделив их затем на dv, получим
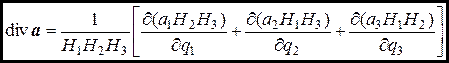 . (9.13)
. (9.13)
 2014-02-12
2014-02-12 475
475








