2014-02-12
1050
Найдем, прежде всего, выражения для элементов длины, площади и объема в ортогональной криволинейной системе координат. Для этой цели рассмотрим бесконечно малый криволинейный параллелепипед, вырезаемый тремя парами координатных плоскостей, отвечающих соответственно значениям параметров q 1, q 2, q 3, равным q 1 и q 1+ dq 1, q 2+ dq 2, q 3+ dq 3 (см. рис. 9.1).
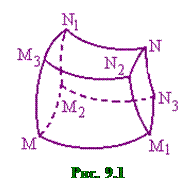Рассмотрим сначала ребро MM 1. Точка M имеет криволинейные координаты (q 1, q 2, q 3), а точка M 1 – криволинейные координаты (q 1+ dq 1, q 2+ dq 2, q 3+ dq 3). Обозначив декартовы координаты точки M 1 – через (x + dx, y + dy, z + dz), мы можем написать, что длина dl 1 вектора 
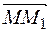равна
.
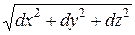Вдоль ребра MM 1 координаты x, y, z суть функции переменной q 1 (переменные q 2 и q 3 постоянны вдоль ребра MM 1). Следовательно, в данном случае
, 
, 
,
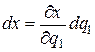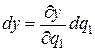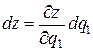и
.
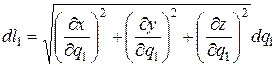Аналогично получаем формулы для длин dl 2 и dl 3 ребер MM 2 и MM 3. Запишем формулы для dl 1, dl 2 и dl 3 следующим образом:
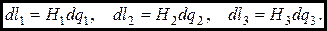(9.6)
Поскольку рассматриваемая система координат ортогональна, то площадь d s1 грани MM 2 N 1 N 2 равна произведению dl 2 на dl 3, т.е.
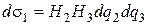, (9.7)
Аналогично получаем для площадей d s2 и d s3 двух других граней MM 1 N 2 M 3 и MM 1 N 3 M 2:
|
|
|
, 
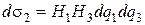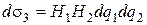(9.8)
Наконец, объем всего рассматриваемого бесконечно малого параллелепипеда равен:
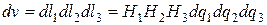, (9.9)
