ЛЕКЦИЯ
Кафедра безопасности жизнедеятельности и медицины катастроф
УНИВЕРСИТЕТ имени И.М. СЕЧЕНОВА
ПЕРВЫЙ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ
Уравнение неразрывности в гидравлической форме (уравнение постоянства расхода)
Понятие живого сечения смоченного периметра и гидравлического (или эквивалентного диаметра).
Напорные, безнапорные потоки и струи.
Различают:
1) напорные;
2) безнапорные потоки и струи.
 |
Струи это потоки, ограниченные только жидкой газообразной средой.
|
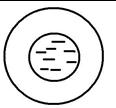
Живое сечение в трубе совпадает с геометрическим.
Живое сечение в струе представляется следующим образом.
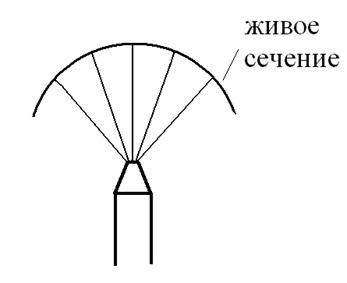
|
1) Для напорного течения смоченный периметр в круглой трубе
c = p×D
2) Для безнапорного течения смоченный периметр
c = np×D, где п < 1

|
|
|
|
Для круглой трубы гидравлический диаметр равен диаметру трубы:
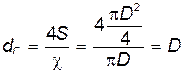
Понятие гидравлического радиуса.
Это понятие используется главным образом у русловиков, т.е, в случае безнапорных течений
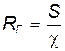 .
.
Для круглой трубы
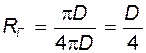
Т.е. гидравлический диаметр равен четырем гидравлическим радиусам R = D /4.
|
Различают объемный, массовый и весовой расход.
а) Объемный расход
объем жидкости, протекающей за время t ,
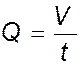 =
= 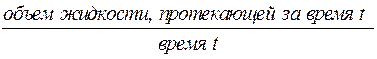
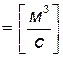
б) Массовый расход
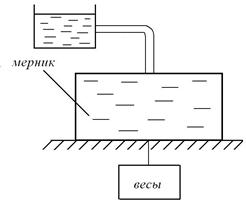
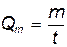 =
= 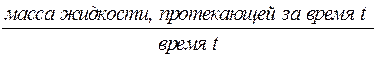
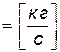
(Если мерник поставить на рычажные весы, то получим массу жидкости)
в) Весовой расход
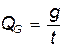 =
= 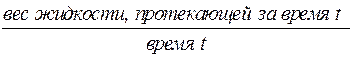
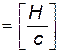
В этом случае мерник надо поставить на пружинные весы.
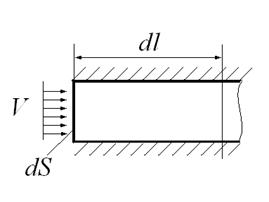 Установим связь расхода со скоростью.
Установим связь расхода со скоростью.
Для элементарной струйки
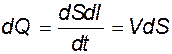
Тогда объемный расход Q через живое сечение равен
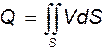
Массовый расход
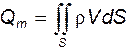
Весовой расход
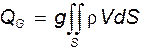
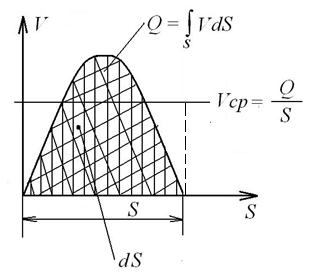 Средняя скорость может быть определена с использованием теоремы о среднем
Средняя скорость может быть определена с использованием теоремы о среднем
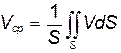
Объемный расход может быть выражен через среднюю скорость следующим образом
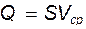
Под гидравлической формой уравнения неразрывности понимаются одномерные подходы, т.е. в этом случае предполагается, что по сечению потока все параметры одинаковы (скорость, давление и пр.). Иначе говоря, речь здесь идет о так называемом стержневом сечении.
Альтернативой гидравлическому подходу является гидродинамический подход, в которой принимается во внимание изменение параметров по сечению потока.
Возьмем два сечения в потоке несжимаемой жидкости для элементарной струйки тока.
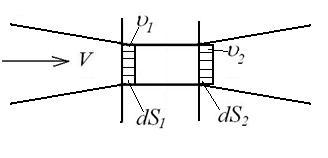
Используя свойство элементарной струйки, что расход в ней не изменен, можно записать
|
|
|
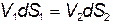
Интегрируя по всему сечения потока, состоящему из элементарных струек можно записать
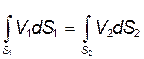
Вводя средние скорости по сечению можно записать
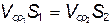 (3.4)
(3.4)
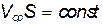 (3.5)
(3.5)
Уравнения (3.4) и (3.5) представляют собой уравнение неразрывности в гидравлической форме для несжимаемой жидкости. Из уравнения неразрывности (3.4) следует, что
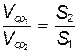 , (3.6)
, (3.6)
т.е., что средняя скорость для несжимаемой жидкости обратно пропорциональна площадям сечения.
Если жидкость сжимаема, то уравнение неразрывности примет вид
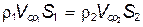
или
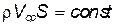
Из последних уравнений следует, что можно ускорять поток, подводя тепло. В этом случае плотность газа уменьшается, а значить скорость должна увеличиваться. Такого рода ускорение потока можно реализовывать только до скорости звука. Дальше закономерности течения уже не описываются указанными уравнениями, поскольку возникают так называемые скачки уплотнения и т.д.
Лечебный факультет
УТВЕРЖДАЮ
Заведующий кафедрой безопасности
жизнедеятельности и медицины
катастроф
профессор, д.м.н., чл.-корр. РАМН
И.М.Чиж
«___»____________2013 г.
Тема № 8. Безопасность фармацевтического труда
для студентов фармацевтического факультета
Обсуждена на заседании
кафедры
«__»___________2013 г.
Протокол №____
Москва – 2013
СОДЕРЖАНИЕ
| № п/п | Учебные вопросы | Время (мин) |
| Введение | ||
| 1. | Характеристика угроз жизни и здоровью фармацевтических работников | |
| 2. | Нормативное правовое регулирование мероприятий по охране труда и технике безопасности | |
| 3. | Система охраны труда и безопасности в фармацевтических организациях | |
| Заключение |
 2014-02-12
2014-02-12 688
688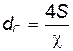 .
.







