Интегрирование некоторых классов трансцендентных функций
a) 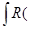 sin x, cos x) dx
sin x, cos x) dx
Универсальная тригонометрическая подстановка 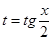 , x=2 arctg t,
, x=2 arctg t,
sin x =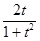 , cos x =
, cos x = 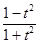 . Нередко к цели быстрее ведут подстановки t=sin x, t=cos x, t = tg x.
. Нередко к цели быстрее ведут подстановки t=sin x, t=cos x, t = tg x.
б) 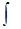 sinmx cosnx dx, m и n – рациональные.
sinmx cosnx dx, m и n – рациональные.
Замена t = sin x ( или t = cos x), cos x = 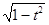 , dt =
, dt =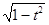 dx, тогда
dx, тогда
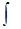 sinmx cosnx dx =
sinmx cosnx dx = 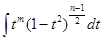 .
.
с) Интегралы вида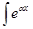 cos bx dx,
cos bx dx, 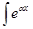 sin bx dx,
sin bx dx, 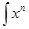 arccos bx dx,,
arccos bx dx,,
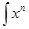 arcsin bx dx,
arcsin bx dx, 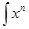 arctg bx dx,
arctg bx dx, 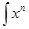 arcctg bx dx,
arcctg bx dx, 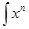 ln x dx вычисляются методом интегрирования по частям.
ln x dx вычисляются методом интегрирования по частям.
а) Дифференциальные биномы
(a+bxn)pxm, когда не является целой ни одна из трех дробей p, 
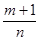 ,
, 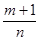 +p.
+p.
б) Интеграл 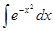 .
.
в) Интегралы вида 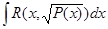 , где - многочлен степени 3, 4 в ряде случаев не выражается через элементарные функции (эллиптические интегралы). В частности, следующие интегралы не являются элементарными функциями
, где - многочлен степени 3, 4 в ряде случаев не выражается через элементарные функции (эллиптические интегралы). В частности, следующие интегралы не являются элементарными функциями
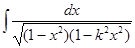 ,
, 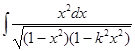 , 0<k<1;
, 0<k<1;
или (после замены)
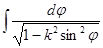 ,
, 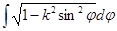 .
.
 2014-02-12
2014-02-12 1530
1530







