I. Дроби вида 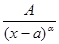 .
.
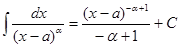 для a¹1 и
для a¹1 и 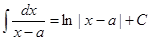
II. Дроби вида 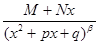 .
.
1) b=1
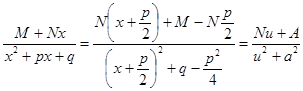 , где u=x+p/2,a2=q - p2/4. Далее
, где u=x+p/2,a2=q - p2/4. Далее 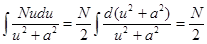 ln (u2+a2 ) +С.
ln (u2+a2 ) +С.
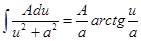 +C.
+C.
2) b>1.
Рассмотрим интегралы вида 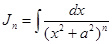 . Интегрируя по частям, получим
. Интегрируя по частям, получим
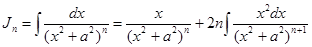 =
=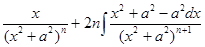 =
=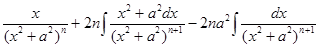 =
=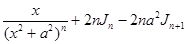 .
.
Откуда получаем рекуррентное соотношение
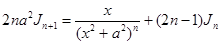 ,
, 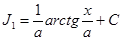 ,
,
позволяющее вычислять интегралы Jn.
§4 Интегрирование некоторых иррациональностей
1. 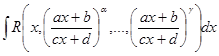
Через R(u,v,…,w) здесь обозначается рациональная функция, то есть выражение, которое может быть получено с помощью конечного числа операций сложения и деления над выражениями u,v,…,w и произвольными константами. Отметим, что суперпозиция рациональных функций будет также рациональной функцией. Дифференциал от рациональной функции равен рациональной функции, умноженной на дифференциал независимого переменного.
Пример рациональной функции
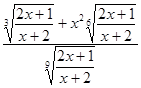 =
=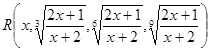 .
.
Интегралы такого вида приводятся к интегралам от рациональных функций с помощью замены 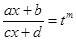 , m – общий знаменатель дробей a,…,g (берут наименьшее общее кратное знаменателей этих дробей). В рассмотренном выше примере, наименьшее общее кратное m=18.
, m – общий знаменатель дробей a,…,g (берут наименьшее общее кратное знаменателей этих дробей). В рассмотренном выше примере, наименьшее общее кратное m=18.
2.Интегралы вида 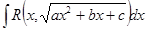 . Подстановки Эйлера
. Подстановки Эйлера
a ) a>0, 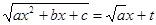
В этом случае ax2+bx+c=ax2+2 xt+t2, откуда
xt+t2, откуда 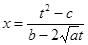 -рациональная функция. Таким образом, подинтегральное выражение примет вид
-рациональная функция. Таким образом, подинтегральное выражение примет вид
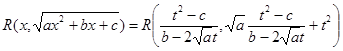 = R1(t) -рациональная функция от t. Кроме того dx=R2(t)dt.
= R1(t) -рациональная функция от t. Кроме того dx=R2(t)dt.
b) Корни x1,x2 квадратного трехчлена ax2+bx+c вещественные, тогда ax2+bx+c =a(x - x1)(x - x2).
Если x1 = x2, то 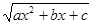 =
= | x – x1| и иррациональность отсутствует. Если x1 ¹ x2, то полагают
| x – x1| и иррациональность отсутствует. Если x1 ¹ x2, то полагают 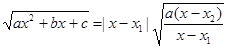 и задача сводится к ранее рассмотренной
и задача сводится к ранее рассмотренной
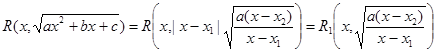 .
.
В этом случае можно так же сделать замену 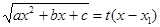 .
.
c) c>0
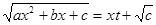 . В этом случае
. В этом случае
ax2+bx+c= x2t2+2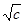 xt+ с, ax+b= xt2 +2
xt+ с, ax+b= xt2 +2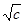 t,
t, 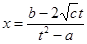 - рациональная функция. После замены получим
- рациональная функция. После замены получим
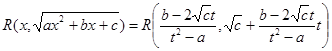 = R1(t) - рациональная функция от t, dx=R2(t)dt.
= R1(t) - рациональная функция от t, dx=R2(t)dt.
Можно показать, что этими тремя подстановками исчерпываются всевозможные случаи. Действительно, если a<0 и c<0 и действительных корней нет, то выражение ax2+bx+c=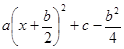 < 0 для всех x и область определения выражения
< 0 для всех x и область определения выражения 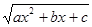 пуста.
пуста.
3. Интегрирование дифференциальных биномов 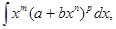 m, n, p – рациональные числа.
m, n, p – рациональные числа.
Сделаем замену x=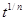 , xm(a+bxn)pdx=
, xm(a+bxn)pdx=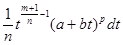 . Таким образом, задача свелась к интегрированию биномов вида
. Таким образом, задача свелась к интегрированию биномов вида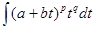 . Интегралы можно вычислить в следующих трех случаях:
. Интегралы можно вычислить в следующих трех случаях:
а) p – целое (a+bt)p tq=R(t, tq )
б) q – целое (a+bt)p tq=R(t, (a+bt)p)
в) p+q – целое (a+bt)p tq=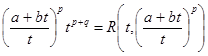
 2014-02-12
2014-02-12 434
434







