Індивідуальні завдання

Відповідності. Функції. Відображення

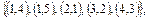
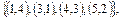
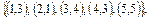
2. Заданы множества кортежей: 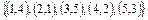. Показать, что эти множества представляют собой соответствия между множествами N ₁ и N ₂, если N ₁ = N ₂ = 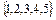. Дать полную характеристику этих соответствий.

□ Найдем декартово произведение:

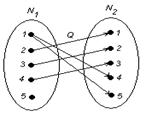
Видно, что заданные множества являются подмножествами этого прямого произведения. Следовательно, данные множества есть соответствия.

а) .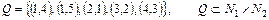

Область определения: 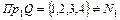. Следовательно, соответствие является частично определенным.

Область значений: 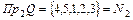. Следовательно, соответствие является сюръективным.

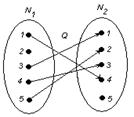Образом элемента 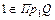являются два элемента 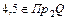. Значит соответствие не является функциональным. Из этого следует, что соответствие не является функцией, отображением.

б) .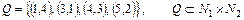

Область определения: 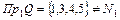. Следовательно, соответствие является частично определенным.

Область значений: 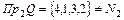. Следовательно, соответствие не является сюръективным.

Образом любого элемента из 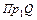является единственный элемент из 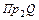. Следовательно, соответствие является функциональным, функцией. Соответствие является частично определенным. Это означает, что функция является частично определенной и не является отображением.

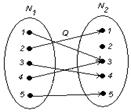в) .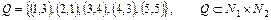

Область определения: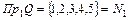.Следовательно, соответствие всюду определено.

Область значений: 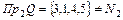. Следовательно, соответствие не является сюръективным.

Образом любого элемента из 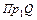является единственный элемент из 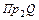. Следовательно, соответствие является функциональным, функцией. Так как соответствие всюду определено, то имеем полностью определенную функцию, т.е. имеем отображение N ₁ в N ₂.

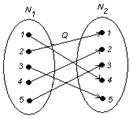г) .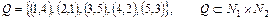

Область определения: 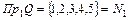. Значит, соответствие полностью определено.

Область значений: 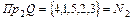. Значит, соответствие сюръективно.

Образом любого элемента из N ₁ является единственный элемент из N ₂. Следовательно, соответствие является функциональным, функцией.

Так как соответствие всюду определено, сюръективно, функционально и прообразом любого элемента из 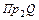является единственный элемент из 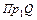, то соответствие является взаимно однозначным.

Так как функция полностью определена и соответствие сюръективно, то имеем отображение N ₁ на N ₂.

Так как для любых двух различных элементов из N ₁ их образы из N ₂ также различны, то отображение является инъективным.

Так как отображение является одновременно сюръективным и инъективным, то имеем биективное отображение (взаимно однозначное отображение).

Необхідна інформація: кортеж, декартово произведение множеств, соответствие, области определения и значений, образ элемента, прообраз, частично и полностью определенное, сюръективное, инъективное, биективное (взаимно однозначное) функциональное, взаимно однозначное соответствия, отображение, функция, отображение «на» и «в».