Машина Тьюринга имеет три алфавита:
1. Внешний алфавит с пустым символом -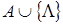
2. Внутренний алфавит, или алфавит состояний  .(Состояние
.(Состояние 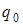 называется заключительным состоянием,
называется заключительным состоянием, 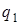 - начальным состоянием, состояния
- начальным состоянием, состояния 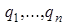 рабочими состояниями.)
рабочими состояниями.)
3. Алфавит сдвигов S = {-1, 0, +1}.
В конструкции машины имеются:
а) бесконечная лента (разбитая на ячейки), предназначенная для размещения бесконечных записей конечных слов над алфавитом А (по одной букве в ячейке);
б) считывающе-записывающее устройство (СЗУ). СЗУ обладает способностью обозревать одну ячейку ленты, считывать букву, записанную в ячейке, заносить на место считываемой буквы любую другую из 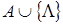 , передвигаться вдоль ленты влево и вправо на одну ячейку;
, передвигаться вдоль ленты влево и вправо на одну ячейку;
в) устройство управления (УУ), которое управляет с помощью программы машины ее работой;
г) программа машины, определяющая переходы машины от одной конфигурации к другой.
Под конфигурацией машины понимают пару: слово с отметкой и состояние машины.
Словом с отметкой называют слово, записанное на ленте с указанием обозреваемой СЗУ ячейки.
Программа машины - отображение П: 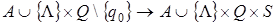 , т. е. правило, сопоставляющее любой паре
, т. е. правило, сопоставляющее любой паре 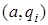 - « буква-состояние» - тройку
- « буква-состояние» - тройку 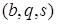 - « буква-состояние-сдвиг». Так как A, Q - конечны, то программу машины можно задать таблицей (см. табл. 15.1).
- « буква-состояние-сдвиг». Так как A, Q - конечны, то программу машины можно задать таблицей (см. табл. 15.1).
Таблица 15.1.
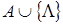 | 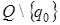 | ||||
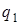 | … | 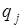 | … | 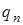 | |
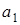 | |||||
| … | … | … | … | … | … |
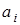 | 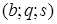 | ||||
| … | … | … | … | … | … |
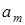 | |||||
| Λ | |||||
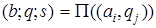 |
Правила работы машины (правила обращения УУ с программой и СЗУ)
Машина работает дискретно (пошагово). На каждом шаге происходит переход от одной конфигурации к другой. Перед началом работы машина находится в начальной конфигурации: СЗУ обозревает первую букву слова, а машина находится в начальном состоянии 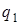 . СЗУ считывает букву, находящуюся в обозреваемой ячейке. УУ обращается к программе машины: находит клетку, соответствующую считанной букве и состоянию машины. Пусть в этой клетке находится тройка
. СЗУ считывает букву, находящуюся в обозреваемой ячейке. УУ обращается к программе машины: находит клетку, соответствующую считанной букве и состоянию машины. Пусть в этой клетке находится тройка 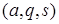 , тогда буква а заносится в обозреваемую ячейку, машина переводится в состояние q, а СЗУ совершает сдвиг на одну ячейку влево, если
, тогда буква а заносится в обозреваемую ячейку, машина переводится в состояние q, а СЗУ совершает сдвиг на одну ячейку влево, если 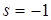 , на одну ячейку вправо, если s = +1, и остается на месте, если
, на одну ячейку вправо, если s = +1, и остается на месте, если 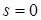 . На этом завершена работа машины на первом шаге, и она готова к выполнению следующего аналогичного шага и т. д.
. На этом завершена работа машины на первом шаге, и она готова к выполнению следующего аналогичного шага и т. д.
Работа машины продолжается до тех пор, пока на каком-то из шагов машина не придет в состояние 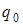 . Устройство управления в этом случае останавливает машину. Возникшая конфигурация называется заключительной, а полученное слово - результатом применения машины к исходному слову.
. Устройство управления в этом случае останавливает машину. Возникшая конфигурация называется заключительной, а полученное слово - результатом применения машины к исходному слову.
Если и - исходное слово, Т - машина, то через Т(и) обозначается результат применения машины Т к слову и.
Говорят, что машина Т не применима к слову и, если в процессе применения ее к слову она ни на каком из шагов не приходит в заключительное состояние.
Пример. Построим машину Тьюринга, складывающую натуральные числа, записанные в унарной системе счисления.
Напомним, что 510 = | | | | | унарн. Рассмотрим алфавит 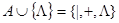 . Необходимо построить машину Т, удовлетворяющую условию:
. Необходимо построить машину Т, удовлетворяющую условию:
Т((т)унарн. + (п)унарн.) = (т + п)унарн.
Такая машина определяется следующей программой:
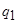 | 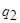 | 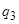 | |
| | |  | 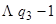 | 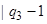 |
| + |  | ||
| Λ | 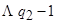 | 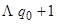 |
Замечание. Условимся составлять программы так, чтобы «останов» происходил на первой букве результата.
Выпишем последовательно возникающие при работе этой машины конфигурации на исходном слове | | + | | |. При записи конфигурации будем использовать следующее соглашение: состояние, в котором находится машина, записывается в круглых скобках справа за обозреваемой ячейкой.
| 0) | 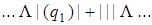 | 8) | 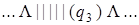 |
| 1) | 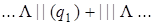 | 9) | 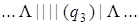 |
| 2) | 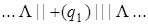 | 10) | 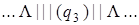 |
| 3) | 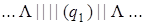 | 11) | 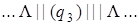 |
| 4) |  | 12) | 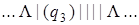 |
| 5) | 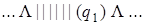 | 13) | 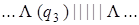 |
| 6) | 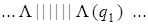 | 14) | 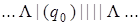 |
| 7) | 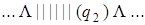 |
Пример. Построить машину Тьюринга, удваивающую натуральные числа, записанные в унарной системе счисления.
Расширим исходный алфавит А = {|} до А' = {|, α }. Искомую машину построим в алфавите 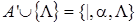 . Ясно, что программа такой машины может выглядеть так:
. Ясно, что программа такой машины может выглядеть так:
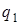 | 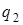 | 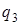 | |
| | | 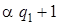 | 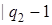 | 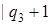 |
| α | 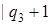 | ||
| Λ | 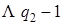 | 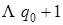 | 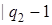 |
Применим полученную машину к слову | |.
| 0) | 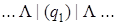 | 5) |  | 10) | 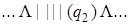 |
| 1) | 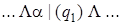 | 6) | 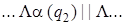 | 11) | 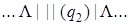 |
| 2) | 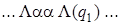 | 7) |  | 12) |  |
| 3) |  | 8) |  | 13) | 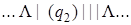 |
| 4) | 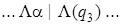 | 9) | 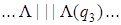 | 14) | 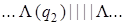 |
| 15) | 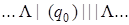 |
Введение новой буквы α и замена исходных | на α позволяет различить исходные | и новые (приписанные) |. Состояние q 1обеспечивает замену | на α, состояние q 2 обеспечивает поиск α, предназначенных для замены на |, и останов машины в случае, когда α не обнаружен, q 3 обеспечивает дописывание | в случае, когда произошла замена α на |.
Введем в рассмотрение стандартные машины:
1. Тождественная машина Е - применима к любому слову над алфавитом А и Е(и) = и.
2.Пусть А - алфавит и 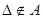 ,
, 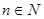 . Копирующей машиной называется машина, применимая к любому слову и над А, причем
. Копирующей машиной называется машина, применимая к любому слову и над А, причем
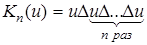
3. Пусть А - алфавит и  . Машиной, заменяющей α на β, называется машина
. Машиной, заменяющей α на β, называется машина 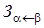 , применимая к любому слову и так:
, применимая к любому слову и так:
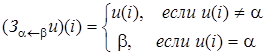
4. Пусть А - алфавит и 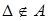 . Машиной-проектором
. Машиной-проектором 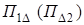 называют машину, применимую к любому слову
называют машину, применимую к любому слову  , где и, v - слова над алфавитом А, причем
, где и, v - слова над алфавитом А, причем
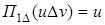 ;
; 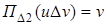 .
.
Теорема 15.3. Тождественная, копирующая, заменяющая машины и машины-проекторы существуют.
15.3. Сочетания машин Тьюринга: композиция и объединение. Машины с полулентами, разветвление и итерация машин
Перечисленные в заголовке типы сочетаний машин позволяют при конструировании машин использовать стандартные приемы, аналогами которых в реальном программировании являются подпрограммы, циклы, разветвления, модульное программирование.
Композиция машин. Композиция машин - последовательное их применение.
Пусть Т 1 - машина с внешним алфавитом А 1 и алфавитом состояний Q 1,
Т 2 - с алфавитами А 2 и Q 2 соответственно, причем 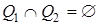 . Композицией Т1 и Т2 называется машина, обозначаемая
. Композицией Т1 и Т2 называется машина, обозначаемая 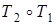 с внешним алфавитом
с внешним алфавитом 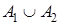 , алфавитом состояний
, алфавитом состояний 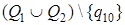 (
( - заключительное состояние Т 1) и работающая по правилу:
- заключительное состояние Т 1) и работающая по правилу:
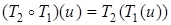
Теорема 15.4. Композиция машин существует.
Пусть программы машин Т 1 и Т 2 выглядят следующим образом:
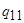 | ……… | 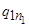 | 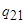 | …….. | 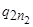 | |||
| А 1 | Т 1 | А 2 | Т 2 |
Программа композиции 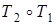 приведена в таблице 15.2.
приведена в таблице 15.2.
Таблица 15.2.
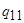 | ……… | 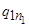 | 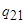 | …….. | 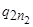 | |||
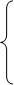 А 1 А 1 |  | |||||||
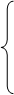 А 2 А 2 | Т 2 | |||||||
Блок 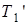 получен из блока T 1 следующим образом: все клетки вида
получен из блока T 1 следующим образом: все клетки вида 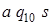 программы Т 1заменены на клетки вида
программы Т 1заменены на клетки вида 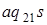 (что и обеспечивает включение в работу машины Т 2 после окончания работы машины Т 1.
(что и обеспечивает включение в работу машины Т 2 после окончания работы машины Т 1.
Пример. Пусть Т 1 - машина, складывающая числа в унарной системе счисления, Т 2 - машина Тьюринга, удваивающая числа, записанные в унарной системе счисления. Тогда 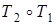 - машина, проводящая вычисления по формуле
- машина, проводящая вычисления по формуле 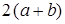 .
.
Машины с полулентами. Прежде чем перейти к объединению, разветвлению, итерации машин, необходимо изучить класс машин Тьюринга с полулентами.
Под машиной с правой (левой) полулентой понимают следующее: в одной из ячеек бесконечной ленты содержится символ ▲ – неподвижный ограничитель, СЗУ машин с правой (левой) полулентой может находиться только на правой (левой) полуленте, состоящей из ячейки, содержащей неподвижный ограничитель, и ячеек, находящихся справа (слева) от этой ячейки.
При выходе СЗУ на ячейку с неподвижным ограничителем мы не имеет права менять ее содержимое. Так как теория машин с левой полулентой - зеркальное отражение теории машин с правой полулентой, мы в дальнейшем будем рассматривать подробно только машины с правыми полулентами.
Теорема 15.5 Пусть▲ T - машина с правой полулентой, тогда существует обычная машина, ей эквивалентная, т. е. для любого слова и над алфавитом А имеет место следующее:
▲ Т (▲ и) = ▲ v → Т(и) = v.
Искомую машину построим в виде композиции трех машин: T 2 ◦▲ T ◦ T 1,
где Т 1 (и) = ▲ и для любого слова и над А, Т 2(▲ и) = v для любого слова ▲ v.
Оказывается, что наряду с этой теоремой справедлива и обратная к ней теорема.
Теорема 15.6. Для любой машины Тьюринга с обычной лентой существует равносильная ей машина с правой (левой) полулентой ▲ T (Т ▲), т. е. для любого слова и над А справедливо следующее:
Т(и) = v → ▲ T (▲ u) = ▲ v.
(T▲ (u ▲) = v ▲)
Расширим исходный алфавит двумя символами: ▲ - неподвижный ограничитель, ∆ - подвижный ограничитель. Искомую машину ▲ T построим в виде композиции ▲ T = T 4 ◦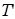 ◦ T 3.
◦ T 3.
Опишем работу машин T 3 и T 4. Машина T 3 применима к любому слову ▲ и и T 3 (▲ и) = ▲ и ∆. Ясно, что T 3 существует. T 4 применима к любому слову
w = ▲ΛΛ…Λ v ∆ и T 4 (w) = ▲ v. Ясно, что и T 4существует. Участок ленты между ▲ и ∆ назовем рабочей зоной. Машина Т ' строится по машине Т следующим образом: внутри рабочей зоны она работает так же, как машина Т, в случае выхода СЗУ на ∆ она перемещает подвижный ограничитель на одну ячейку вправо, помещая в освободившуюся ячейку Λ, и продолжает работу, возвращаясь на одну ячейку влево в том же состоянии, в котором СЗУ вышло на ∆. Эта возможность расширения рабочей зоны обеспечивается введением для каждого рабочего состояния q машины Т состояния  машины Т '.
машины Т '.
Хуже обстоит дело в случае, когда СЗУ выходит на ▲, так как неподвижный ограничитель нельзя перемещать. В этот момент работа машины
Т ' как машины Т должна прерваться для того, чтобы побуквенно переместить слово на одну ячейку вправо, заполнив освободившуюся ячейку пустым символом Λ; после чего машина Т ' может вернуться к освободившейся ячейке и продолжить работу как машина Т. Сложность такой «модернизации» Т к Т ' состоит в том, что машина Тьюринга не обладает внутренней памятью, а запоминать нужно рабочее состояние, в котором произошел выход СЗУ на неподвижный ограничитель и перекладываемые буквы (какую поместить в ячейку из предыдущей и какую запомнить, чтобы переложить в следующую). Такое расширение рабочей зоны обеспечивается введением для каждого рабочего состояния q машины Т целого шлейфа состояний машины Т ' (длина шлейфа зависит от | А|). Выпишем программу машины Т ' в случае, когда А = 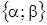 (табл. 15.3).
(табл. 15.3).
Таблица 15.3.
| α | β | Λ | ▲ | ∆ | |
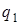 | Т | ▲ q ▲ +1 | Λ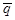 +1 +1 | ||
| … | |||||
| q | |||||
| … | |||||
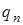 | |||||
| q ▲ | Λ qα +1 | Λ qβ +1 | Λ q Λ +1 | ∆ q ∆ +1 | |
| qα | α qα +1 | α qβ +1 | α q Λ +1 | α q ∆ +1 | |
| qβ | β qα +1 | β qβ +1 | β q Λ +1 | β q ∆ +1 | |
| q Λ | Λ qα +1 | Λ qβ +1 | Λ q Λ +1 | Λ q ∆ +1 | |
| q ∆ | ∆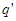 -1 -1 | ||||
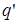 | α 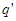 -1 -1 | β 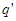 -1 -1 | Λ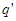 -1 -1 | ▲ q +1 | |
 | ∆ q -1 |
Очевидно, построение программы Т 'возможно в случае любого конечного алфавита А.
Доказанные две теоремы означают, что класс машин с полулентами эквивалентен классу обычных машин Тьюринга.
Объединение машин
Пусть Т 1 и Т 2 - машины Тьюринга с общим или различными внешними алфавитами А 1, А 2и пусть▲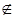 А 1
А 1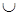 А 2.
А 2.
Объединением машин Т 1 и Т 2 называется машина, обозначаемая 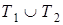 , работающая по правилу
, работающая по правилу
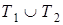 (и ▲ v) =
(и ▲ v) =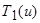 ▲
▲ 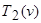 .
.
Теорема 15.7. Объединение машин существует.
Объединение построим в виде композиции четырех машин:
Т +▲ о ▲ Т 2 о Т ▲+ о Т 1▲,
где Т 1▲ - аналог машины Т 1на левой полуленте, ▲ Т 2 - аналог машины Т 2 на правой полуленте. машина Т ▲+, отправляясь от первой буквы слова w ▲ z, останавливается на первой букве после символа ▲, оставляя на ленте слово w ▲ z. Машина Т +▲, отправляясь от первой справа за ▲ буквы слова w ▲ z, останавливается на первой букве слова w, оставляя на ленте слово w ▲ z. Очевидно, машины Т ▲+ и Т +▲ существуют.
Разветвление машин
Пусть Т 1 и Т 2 - две машины Тьюринга с общим внешним алфавитом А и алфавитами состояний Q 1 и Q 2 (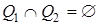 ) и пусть 0 и 1 не принадлежат А.
) и пусть 0 и 1 не принадлежат А.
Пусть Ф - машина-предикат, т. е. машина с внешним алфавитом {0; 1}, применимая к любому слову и над алфавитом А и Ф(и) принадлежит множеству {0;1}.
Разветвлением машин Т 1, Т 2, управляемым предикатом Ф, называется машина, обозначаемая 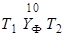 , которая работает по правилу
, которая работает по правилу
(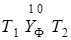 )(и)=
)(и)=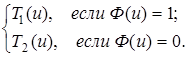
Теорема 15.8. Разветвление машин существует.
Построим разветвление в виде композиции трех машин
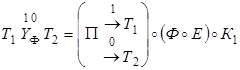 ,
,
где машина 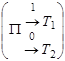 имеет программу, представленную в виде табл. 15.4
имеет программу, представленную в виде табл. 15.4
Начальным состоянием машины  является состояние
является состояние 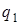 , а заключительными - заключительные состояния
, а заключительными - заключительные состояния  ,
, 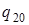 - машин Т 1 и Т 2соответственно.
- машин Т 1 и Т 2соответственно.
Таблица 15.4.
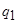 | 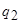 | 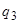 | 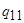 | ……… | 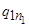 | 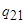 | …….. | 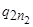 | |
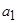 | |||||||||
| …….. | Т 1 | Т 2 | |||||||
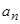 | |||||||||
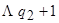 | |||||||||
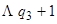 | |||||||||
| ▲ | 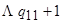 | 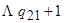 |
Итерация машины. Пусть Т - машина Тьюринга с внешним алфавитом А и Ф – машина-предикат.
Итерацией машины Т по предикатуФ называется машина, обозначаемая ТФ, работа которой описывается следующим образом:
1. К слову и применяется предикат Ф, если Ф (и) = 1, то переход к 2, если Ф (и)= 0, то переход к 3.
2. 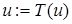 , переход к 1.
, переход к 1.
3. (ТФ)(и):= и, останов.
Теорема 15.9. Итерация машины Т по предикату Ф существует.
Построим машину 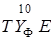 . Обозначим через (
. Обозначим через (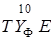 ) ' машину, программа которой получается из программы
) ' машину, программа которой получается из программы 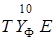 следующей модернизацией: все клетки, содержащие тройки
следующей модернизацией: все клетки, содержащие тройки 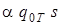 , где
, где 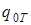 - заключительное состояние машины Т,заменяются на клетки, содержащие
- заключительное состояние машины Т,заменяются на клетки, содержащие 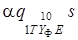 , где
, где 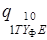 - начальное состояние всего агрегата
- начальное состояние всего агрегата 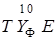 . Очевидно, ТФ = (
. Очевидно, ТФ = (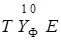 ) '.
) '.
 2014-02-12
2014-02-12 6665
6665
