Состояния. Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных

Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой автомата. В комбина­ционных схемах промежуточные переменные непосредственно не участвуют в соотношениях «вход-выход». Напротив, выходные функции последовательностных схем в качестве своих аргументов, кроме входных переменных, обязательно содержат некоторую сово­купность промежуточных переменных 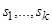, характеризую­щих состояние схемы. Набор всех возможных состояний, которые присущи данной схеме, называется множеством состояний. Если 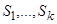- конечные алфавиты переменных состояния 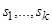, то множество состояний 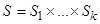, также явля­ется конечным множеством.

Строгое определение понятия состояния связывается с той ролью, которое оно играет при описании конечных автоматов. Во-первых, значения совокупности выходных переменных на v-м такте 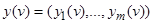однозначно определяется значениями входных переменных 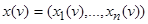и состоянием 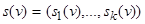на том же такте, т.е. 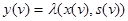. Во-вторых, состояние s(v+1) в следующем (v + 1)-м такте одно­значно определяется входными переменными x(v) и состоянием s(v) в предыдущем такте, т. е. .

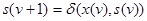Таким образом, состояние конечного автомата в любой тактовый момент характеризуется значениями такой совокупности перемен­ных, которая вместе с заданными значениями входных переменных позволяет определить выходные переменные и данный тактовый момент и состояние в следующий тактовый момент.

Ясно, что последовательностные схемы должны обладать способ­ностью сохранять предыдущее состояние до следующего такта, в связи с чем их называют также автоматами с памятью или последовательностными машинами.