ЗАДАЧИ
Выводы
Одноступенчатый метод при прочих равных условиях обеспечивает минимальную продолжительность испытаний.
Двухступенчатый метод при тех же условиях обеспечивает минимальный средний объем испытаний.
ТЕМА: РАСЧЕТ ВЕРОЯТНОСТИ БЕЗОТКАЗНОЙ РАБОТЫ
Задача 1
Наработка системы до отказа описывается экспоненциальным распределением с параметров λ = 1*10-4r-1.
Определить вероятность безотказной работы Р(t1) и плотность распределения f(t1) при t1=2000ч, а также среднюю наработку до отказа T
Решение
согласно Р(t1)=е-λt
Р(2000)=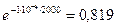
согласно f (t)= λе-λt
f(2000)= 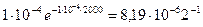
согласно T = 1/λ=1*104r
Задача 2
Рассчитать вероятности безотказной работы за 2000ч. Р(2000) системы регулирования уровня при следующих вероятностях безотказной работы элементов.
РFb = РFn = Ре=0,94 Р3d=0,99 Рр=0,93 Рим=0,92 Рро=0,74
Решение
Структурные схемы
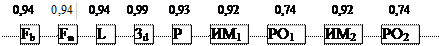 а)
а)
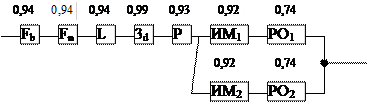 б)
б)
Fb, Fn – расходомеры питательной воды и пара.
L – уровнемер; 3d – задатчик уровня, Р – регулирующий прибор; ИМ – исполнительный механизм.
РО – регулирующий орган.
Схема а)
Так как элементы соединены последовательно, то для определения вероятности безотказной работы системы необходимо перемножить вероятности безотказной работы элементов соединений последовательно
Рс(2000) = 0,943*0,99*0,93*0,922*0,742=0,35
Схема б)
Если для работы системы достаточного одного регулирующего органа, то вероятность безотказной работы системы регулирования уровня
Рс(2000) = 0,943*0,99*0,93(1-(1-0,92*0,74)2)=0,69.
Так как структурная схема надежности параллельно последовательная, то в этом случае умножаются вероятности отказов:
 |
Р (t)+Q(t)=1.
Вероятность безотказной работы одной цепи Р1(t)=0,92*0,74
Вероятность отказа Q1(t)=1-0,92*0,74
Вероятность отказа двух ветвей 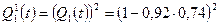
Тогда вероятность безотказной работы двух ветвей Р1(t)=1-(1-0,92*0,74)2.
Таким образом, использование резерва по регулирующему органу с исполнительным механизмом, являющихся наименее надежными элементами обеспечивается повышение вероятности безотказной работы до 2000 часов с 0,35 до 0,69.
ТЕМА: ПЛАНЫ ИСПЫТАНИЙ НА НАДЕЖНОСТЬ
Задача № 1
Испытание систем на безотказность, проведение по плану [NUN], где N=15, показали следующие наработки на отказ:
ti = 922,766,153,250,604,553,731,411,505,310,140,214,308,415,981
Найти точечную оценку и доверительные границы средней наработки до отказа с доверительной вероятностью γ=0,9.
Решение
Планы испытаний:
1. N – число испытываемых систем
2. R – наличие восстановлений во время испытаний при наличии отказа
U - отсутствие восстановлений во время испытаний при наличии отказа.
3. – критерий прекращения испытаний:
NUN – испытывается N систем, восстановление систем отсутствует, испытания прекращаются при отказе N систем.
1. Точечная оценка средней наработки до отказа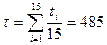 часов
часов
2. Оценка среднеквадратического отклонения средней наработки до отказа для плана NUN
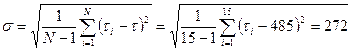 часа
часа
3. Оценка коэффициента вариации 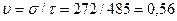
4. Относительное значение нижней границы доверительного интервала
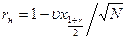 , где
, где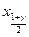 доверительный интервал величины при доверительной вероятности γ
доверительный интервал величины при доверительной вероятности γ
α-квантиль нормального распределителя
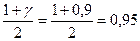 , т.е. α = 0,95
, т.е. α = 0,95
Некоторые значения квантилей
| α | 0,5 | 0,7 | 0,8 | 0,9 | 0,95 | 0,97 | 0,99 |
| Хα | 0,524 | 0,842 | 1,282 | 1,645 | 1,881 | 2,326 |
т.е. Х0,95=1,645. тогда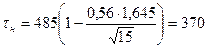 час.
час.
5. Относительное значение верхней границы доверительного интервала: Твр=t*rвр; 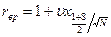 . Тогда
. Тогда 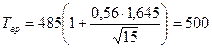 часов.
часов.
Таким образом, можно сказать, что средняя наработка на отказ составляет 485 часов, и с доверительной вероятностью 0,9, минимальное время наработки до отказа 370 часов, максимальное время наработки до отказа 500 часов.
Задача № 2
При испытаниях N=20 восстанавливаемых систем по плану [NRT] получено n∑=10 отказов. Длительность испытаний Т=1000 часов. Найти точечную оценку и доверительные границы параметра потока отказов и средней наработки на отказ при доверительной вероятности γ =0,8. Применимость простейшего потока предполагается доказанной.
Решение
Испытывается 20 систем, R - предполагается восстановление во время испытания 1000 часов.
1. Точечная оценка параметра потока отказов
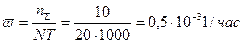
2. Нижняя граница параметра потока отказов
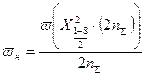 ,
,
где 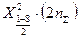 – квантиль Х2-распределения при вероятности
– квантиль Х2-распределения при вероятности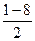 и числом степеней свободы 2n∑ (выбирается из спец таблиц).
и числом степеней свободы 2n∑ (выбирается из спец таблиц). 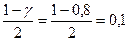 ; n∑=10
; n∑=10
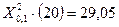 .
.
Тогда 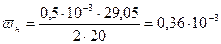 1/час
1/час
3. Верхняя граница параметра потока отказов
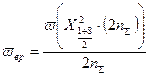
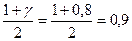
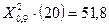
Задача № 3
При испытаниях N=10 систем по плану [NRT] не было получено отказов. Длительность испытаний Т=1000 часов. Найти доверительные границы параметра потока отказов и средней наработки на отказ при доверительной вероятности γ =0,95. Применимость простейшего потока предполагается доказанной.
Решение
Так как отказов не было, нижняя доверительная граница потока отказов ωн=0.
Верхняя доверительная граница потока отказов в этом случае определяется
ωвр=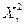 (2)/2NT=5,99/2*10*1000=3*10-4 1/час
(2)/2NT=5,99/2*10*1000=3*10-4 1/час
Верхняя односторонняя доверительная граница средней наработки на отказ 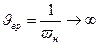 не определяется.
не определяется.
Нижняя односторонняя доверительная граница средней наработки на отказ
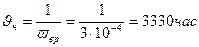
 2014-02-12
2014-02-12 2539
2539







