2014-02-13
969
Рассмотрим отдельно дифференциал и, применяя метод обращения движения - остановки водила, преобразуем его в передачу с неподвижными осями вращения колес. Составим таблицу угловых скоростей центральных звеньев, как в заданном, так и в преобразованном механизме:
Таблица № 1
| Звенья Тип движения | Центральные звенья | ||
| «в» | |||
| Действительное | ω1 | ω3 | ωв |
| Дополнительное | –ωв | –ωв | –ωв |
| Суммарное | ω1–ωв | ω3–ωв |
Для приведенного механизма найдем отношение угловых скоростей центральных звеньев, которое выразим через радиусы колес:
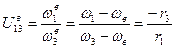
Делим почленно числитель и знаменатель третьего члена на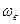 
: 
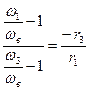
Откуда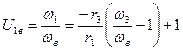 
Далее рассматриваем замыкающую цепь, выполненную в виде простого планетарного механизма. Так же применяем метод остановки водила, и составляем таблицу:
Таблица № 2
| Звенья Тип движения | Центральные звенья | ||
| «а» | |||
| Действительное | ω4=0 | ω6 | ωа |
| Дополнительное | –ωа | –ωа | –ωа |
| Суммарное | –ωа | ω6–ωа |
Для приведенного механизма находим отношение угловых скоростей центральных звеньев, которое выражаем через радиусы колес:
|
|
|
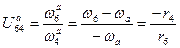
Делим почленно числитель третьего члена на его знаменатель: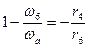 
.
Откуда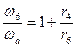 
Учитывая, что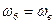 
и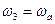 
перепишем уравнение в следующем виде:
С учетом того, что 
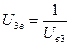подставим полученное значение передаточного отношения замыкающей цепи в полученное выражение для дифференциала и преобразуем полученное выражение:
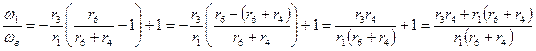
В результате,
