Упорядоченные поля

В некоторых полях, наряду с бинарными операциями сложения и умножения элементов поля, вводятся отношения порядка, определенным образом связанные с бинарными операциями. Такие поля называются упорядоченными.

Определение. Поле называется упорядоченным, если множество его элементов упорядочено и отношение строгого порядка 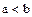удовлетворяет следующим условиям:

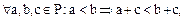(4.16)

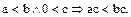(4.17)

Условия (4.16) (4.17) этого определения связывают отношение строгого порядка с бинарными операциями, определенными в поле .

Условие (4.16) называется законом монотонности сложения, а условие (4.17) – законом монотонности умножения.

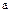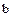Если элемент упорядоченного поля меньше элемента этого поля, то говорят, что элемент в больше чем элемент 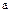, и записывают .

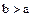Теорема. Элемент 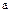упорядоченного поля тогда и только тогда больше элемента 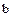этого поля, когда .

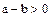Доказательство. В самом деле, если 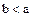, то, в силу условия 1 определения 1, 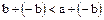, т. е. 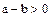. Наоборот, если 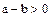, то 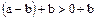, т. е. .

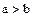Определение. Элемент 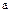упорядоченного поля называют положительным, если 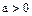, его называют отрицательным, если .

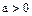Если элемент 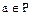положителен, то противоположный ему элемент – а отрицательный, так как из 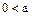, в силу условия 1 определения 1, вытекает, что 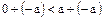, или .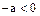

Примерами упорядоченных полей являются поле рациональных и поле действительных чисел. Об этих полях более подробно будет говориться в следующей главе.

Рассмотрим теперь некоторые простейшие свойства упорядоченных полей. Пусть – произвольное упорядоченное поле.

1. Для всяких элементов 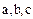упорядоченного поля из соотношений 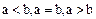вытекают соответственно соотношения .

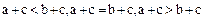Доказательство. В самом деле, в силу условия 1 определения 1, 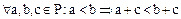. Отсюда следует, что 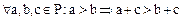. Действительно, 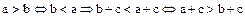. Так как операция сложения во всяком поле однозначна, то .

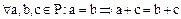2. Для любых элементов 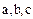упорядоченного поля из соотношений 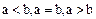вытекают соответственно соотношения 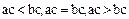, если 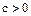, и соотношения 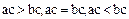, если .

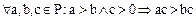Доказательство. В силу условия 2 определения 1, .Отсюда вытекает, что . Действительно, 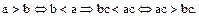Далее, 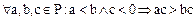и 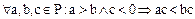. В самом деле, 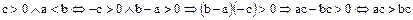. Аналогично,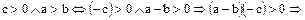 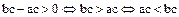. Из однозначности операции умножения в любом поле вытекает, что .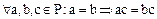

3. Для всяких элементов 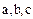упорядоченного поля из соотношений 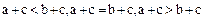вытекают соответственно соотношения .

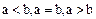Доказательство. Действительно, , , .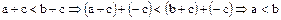

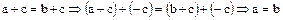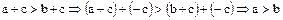4. Для любых элементов 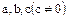упорядоченного поля из соотношений 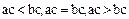вытекают соответственно соотношения 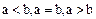, если 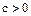, и соотношения 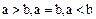, если .

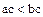Доказательство. Доказывается это свойство методом от противного. Докажем, например, что при из соотношения вытекает соотношение 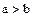. Предположим, что 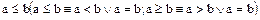. Тогда, в силу 2, 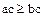, что невозможно, так как по условию 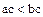. Таким образом, предположение, что 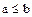приводит к противоречию. Следовательно, 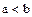. Аналогичные рассуждения проводятся и при рассмотрении всех других случаев.

5. Для любых элементов 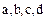упорядоченного поля из соотношений 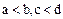вытекает соотношение .

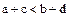Доказательство. 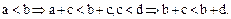Ho .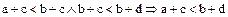

6. Для любых положительных элементов 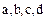упорядоченного поля из соотношений 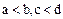вытекает соотношение .

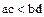Доказательство. В силу условия 2 определения 1, 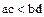, 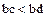и, следовательно, .

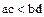Определение. Модулем (или абсолютной величиной) элемента 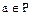называют неотрицательный из элементов 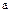и 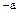. Иными словами, модуль элемента 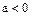– это сам элемент 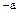, модуль элемента 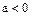– это противоположный элемент 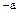. Модуль элемента 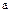обозначают символом .

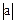В соответствии с определением 3 всегда

.

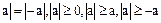7. Для любых элементов 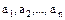упорядоченного поля справедливо соотношение

.

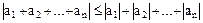Иногда это свойство формулируют следующим образом: модуль суммы конечного числа элементов упорядоченного поля не больше суммы модулей слагаемых.

Доказательство. При 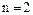это свойство имеет место. Действительно, так как всегда 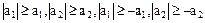, то 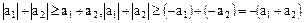. Если 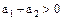, то 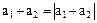и, следовательно, 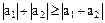. Если же 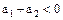, то 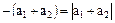и поэтому .

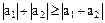Следовательно, всегда .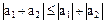

Предположим теперь, что утверждение справедливо для 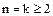, т.е. 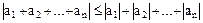. Тогда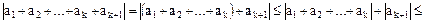 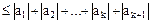, тe. .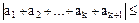

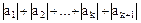Таким образом, из предположения, что утверждение справедливо для 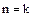, вытекает его справедливость и для 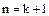. Следовательно, в силу принципа математической индукции, оно справедливо для любого натурального .

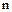8. Для любых элементов 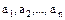упорядоченного поля справедливо соотношение

.

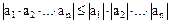Иными словами, модуль произведения конечного числа элементов упоря­доченного поля равен произведению модулей сомножителей. Доказывается это свойство, как и предыдущее, методом математической ин­дукции.

Теорема. Сумма квадратов конечного числа элементов упорядоченного поля , по крайней мере один из которых отличный от нуля, больше нуля.

Доказательство. Если 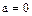, то и 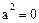. Если же 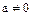, то либо 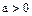, либо 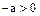. Поскольку 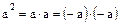, то в обоих случаях, в силу свойства 2, 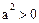. Таким образом, если по крайней мере один из элементов 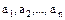, отличный от нуля, то в сумме квадратов этих элементов каждое из слагаемых либо равно нулю, либо больше нуля, но хотя бы одно из них больше нуля. Следовательно, в силу свойства 1,

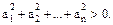
Следствие. Единичный элемент 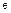упорядоченного поля больше ну­левого элемента 0.

Доказательство. В самом деле.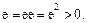

Теорема. Всякое упорядоченное поле есть поле характеристики нуль.

Доказательство. Единичный элемент 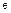поля больше нулевого элемента 0. Поэтому для любого натурального числа 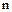кратное .

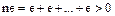Так как 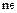– положительный элемент и 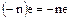, то 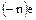– отрицательный элемент, т. е. 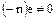. Следовательно, 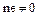при любом целом, отличном от нуля 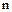, а это и означает, что – поле характеристики нуль.