Структура многоразрядного суммматора с параллельным переносом

Паралельный перенос в i - том разряде многоразрядного сумматора можно определить как функцию разрядов слагаемых i - того, всех младших разрядов и входного переноса. Для организации этого принципа в каждом разряде сумматора должны быть сформированы два дополнительных сигнала (D_i, F_i).

D_i- функция генерации переноса в данном разряде.

F_i - функция распространения переноса через данный разряд

P_i= a_i b_i + p_i (a_i + b_i) = D_i + p_i F_i

С учетом этих значений запишем уравнение, описывающее структуру четырехразрядного паралельного сумматора с паралельным переносом:

P₀ = D₀ + F₀p_вх;

P₁ = D₁ + P₀ F₁ = D₁ + F₁ D₀+ F₀ F₁ p_вх;

P₂= D₂ + P₁ F₂ = D₂ + F₂ D₁+ F₁ F₂ D₀+ F₀ F₁ F₂p_вх;

P₃= D₃ + P₂ F₃ = D₃ + F₃ D₂+ F₂ F₃ D₁+ F₃ F₂ F₁ D₀ + F₃ F₂ F₁F₀p_вх;

D₀ F₀

P₃ = D^/₀ + F^/₀ p_вх;

D^/₀- функция генерации выходного переноса из четырехразрядной секции.

F^/₀ - функция распространения переноса через четырехразрядную секцию.

Схемы ускоренного переноса (СУП) реализованные на данных уравнениях:

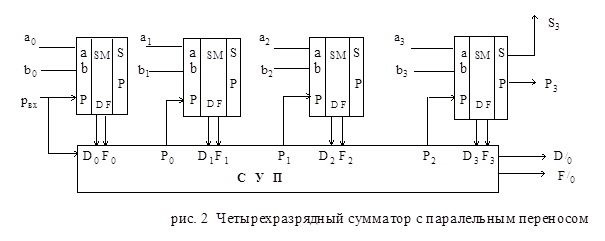
D^/₀и F^/₀используют для дальнейшей наращиваемости.

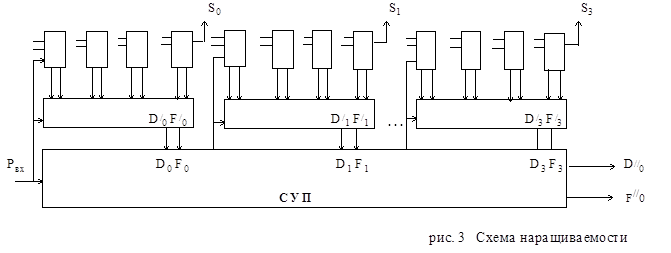
Лекция 2 “Матричные комбинационные умножители”

Процедура умножения это достаточно долгая по времени выполнения команда, поэтому есть смысл реализовать аппаратное умножение с возможностью наращивания операндов.

Различают два типа цифровых умножителей: множительный блок (МБ) и множительно-суммирующий блок (МСБ).

1. Множительный блок (практически никогда не используется): S = A * B;

2. Множительно-суммирующий блок: S = A * B + К + М;

Возьмем максимально большие значения А = В = К = М = 1111, убедимся что

переполнения не происходит:

1 1 1 1