2014-02-13
241
Оценка параметров линейной эконометрической модели
Вид такой модели приводился ранее:
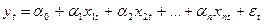(4)
Исходными данными при оценке параметров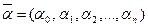 
являются наблюдаемые значения независимой и зависимых переменных
………………………..
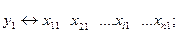
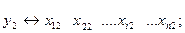
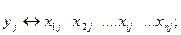(5)
………………………..
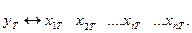
С учетом вида функционала, по которому и определяются частные производные, система (3) дает следующую систему уравнений:
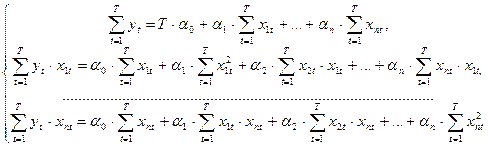(6)
В этой линейной относительно параметров 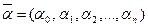системе уравнений коэффициентами являются суммы
, 
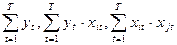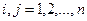, значения которых вычисляются по исходным данным. В случае, когда определитель матрицы этой системы не равен нулю, т.е. система является квадратной и невырожденной, ее решение может быть найдено либо по методу Гаусса, либо по методу Крамера.
Для случая, когда в системе число неизвестных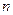 
не совпадает с числом уравнений 
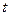, применяют псевдообратные матрицы. Перепишем систему (6) в матричной форме.
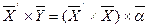, (7)
где через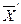 
обозначена матрица транспонированная к 
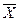. Причем
, 
, 
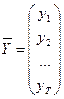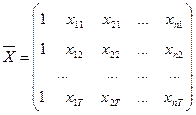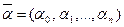(8)
Матрица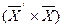 
является уже квадратной и поэтому можно говорить об ее обратимости. В этом случае решение системы в матричной форме находится по формуле:
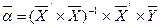(9)
